题目内容
4.在等差数列{an}中,a1<0,S18=S36,若Sn最小,则n的值为( )| A. | 18 | B. | 27 | C. | 36 | D. | 54 |
分析 根据等差数列的性质求出当an<0时,n的取值范围即可得到结论.
解答 解:由S18=S36,得a19+a20+…+a35+a36=0,
即9(a27+a28)=0,即a27+a28=0,
则2a1+53d=0,即d=-$\frac{2}{53}$a1>0,
则an=a1+(n-1)d=a1-$\frac{2}{53}$a1(n-1),
由an=a1-$\frac{2}{53}$a1(n-1)≤0,得1-$\frac{2}{53}$(n-1)≥0,
得2n≤55,得n≤$\frac{55}{2}$=27$\frac{1}{2}$,
即当n≤27时,an<0,
则要使Sn最小,则n=27,
故选:B.
点评 本题主要考查等差数列的性质,结合等差数列的前n项和公式以及性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若α是第二象限角,则$\frac{1}{2}$+$\frac{1}{2}$$\sqrt{\frac{1}{2}+\frac{1}{2}cos2α}$的值等于( )
| A. | cos2$\frac{α}{2}$ | B. | sin2$\frac{α}{2}$ | C. | cos2α | D. | sin2α |
14.关于x的不等式|x-1|-|x-3|>a2-3a的解集为非空数集,则实数a的取值范围是( )
| A. | 1<a<2 | B. | $\frac{{3-\sqrt{17}}}{2}<a<\frac{{3+\sqrt{17}}}{2}$ | C. | a<1或a>2 | D. | a≤1或a≥2 |
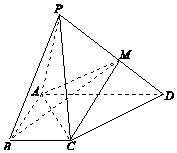 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠DAB=∠ABC=90°,AD=2BC,四棱锥P-ABCD的体积为10,点M在PD上.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠DAB=∠ABC=90°,AD=2BC,四棱锥P-ABCD的体积为10,点M在PD上.