题目内容
8.已知F1,F2为双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=$\frac{1}{3}$,则E的离心率为$\sqrt{2}$.分析 根据双曲线的定义,结合直角三角形的勾股定理建立方程关系进行求解即可.
解答 解:∵MF1与x轴垂直,sin∠MF2F1=$\frac{1}{3}$,
∴设MF1=m,则MF2=3m,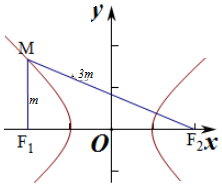
由双曲线的定义得3m-m=2a,即2m=2a,得m=a,
在直角三角形MF2F1中,9m2-m2=4c2,即8m2=4c2,
即8a2=4c2,
即2a2=c2,
则$\sqrt{2}$a=c,
则e=$\frac{c}{a}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题主要考查双曲线离心率的计算,根据双曲线的定义结合直角三角形的勾股定理,结合双曲线离心率的定4义是解决本题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
20.某工厂生产某种产品的产量x(吨)与相应的生产成本y(万元)有如下几组样本数据:
据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得到其回归直线的斜率为0.8,则当该产品的生产成本是6.7万元时,其相应的产量约是( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3.1 | 3.9 | 4.5 |
| A. | 8 | B. | 8.5 | C. | 9 | D. | 9.5 |
3.已知一个平放的正三棱锥型容器的各棱长为6,其内有一小球O(不计重量),现从正三棱锥型容器的顶端向内注水,球慢慢上浮,若注入的水的体积是正三棱锥体积的$\frac{7}{8}$时,球与正三棱锥各侧面均相切(与水面也相切),则球的表面积等于( )
| A. | π | B. | $\frac{3}{2}$π | C. | $\frac{4}{3}$π | D. | $\frac{7}{6}$π |
17.用反证法证明“三角形中至少有一个内角不小于60°”,应先假设这个三角形中( )
| A. | 有一个内角小于60° | B. | 每一个内角都小于60° | ||
| C. | 有一个内角大于60° | D. | 每一个内角都大于60° |