题目内容
4．
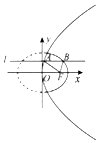如图动直线l：y=b与抛物线y2=4x交于点A，与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B，F为抛物线的焦点，则AF+BF+AB的最大值为（ ）| A． | 3 | B． | $3\sqrt{2}$ | C． | 2 | D． | $2\sqrt{2}$ |
分析 由题意画出图形，结合抛物线的定义及椭圆定义把AF+BF+AB转化求得最大值．
解答 解：如图，
延长BA交抛物线的准线于C，设椭圆的左焦点为F′，连接BF′，
则由题意可得：AC=AF，BF=2a-BF′，
∴AF+BF+AB=AC+2a-BF′+AB=AC+AB+2a-BF′
=BC+2a-BF′=2a-（BF′-BC）．
≤2a=$2\sqrt{2}$．
∴AF+BF+AB的最大值为$2\sqrt{2}$．
故选：D．
点评 本题考查椭圆的简单性质，考查了数形结合的解题思想方法和数学转化思想方法，属中档题．
练习册系列答案
相关题目
14．在空间直角坐标系中，点A（1，-2，3）与点B（-1，-2，-3）关于（ ）对称．
| A． | x轴 | B． | y轴 | C． | z轴 | D． | 原点 |
12．已知A、B、C是圆O上的三个点，CO的延长线与线段BA的延长线交于圆外一点．若$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$，其中m，n∈R．则m+n的取值范围是（ ）
| A． | （0，1） | B． | （-1，0） | C． | （1，+∞） | D． | （-∞，-1） |
19．我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”，设△ABC三个内角A、B、C所对的边分别为a、b、c，面积为S，则“三斜求积”公式为$S=\sqrt{\frac{1}{4}[{{a^2}{c^2}-{{（{\frac{{{a^2}+{c^2}-{b^2}}}{2}}）}^2}}]}$．若a2sinC=4sinA，（a+c）2=12+b2，则用“三斜求积”公式求得△ABC的面积为（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | 3 | D． | $\sqrt{6}$ |
某班级将从甲、乙两位同学中选派一人参加数学竞赛，老师对他们平时的5次模拟测试成绩（满分：100分）进行了记录，其统计数据的茎叶图如图所示，已知甲、乙两位同学的平均成绩都为90分．
14．平面截球得到的半径是3的圆面，球心到这个平面的距离是4，则该球的表面积是（ ）
| A． | 20π | B． | $\frac{416\sqrt{3}π}{3}$ | C． | $\frac{500π}{3}$ | D． | 100π |