题目内容
14.在空间直角坐标系中,点A(1,-2,3)与点B(-1,-2,-3)关于( )对称.| A. | x轴 | B. | y轴 | C. | z轴 | D. | 原点 |
分析 先根据空间直角坐标系对称点的特征,点(x,y,z)关于y轴的对称点的坐标为只须将横坐标、竖坐标变成原来的相反数即可,即可得对称点的坐标.
解答 解:∵在空间直角坐标系中,
点(x,y,z)关于y轴的对称点的坐标为:(-x,y,-z),
∴点A(1,-2,3)与点B(-1,-2,-3)关于y轴对称,
故选B.
点评 本小题主要考查空间直角坐标系、空间直角坐标系中点的坐标特征等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
5.直线3x+4y+a=0上存在点M满足过点M作圆(x-2)2+(y-1)2=2的两条切线互相垂直,则a的取值范围是( )
| A. | (-20,0] | B. | [-20,0] | C. | [-20,0) | D. | (-20,0) |
9.函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则f(x)的解析式是( )
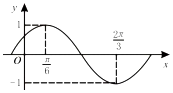

| A. | $f(x)=sin(x+\frac{π}{6})$ | B. | $f(x)=sin(x+\frac{π}{3})$ | C. | $f(x)=sin(2x+\frac{π}{6})$ | D. | $f(x)=sin(2x+\frac{π}{3})$ |
4.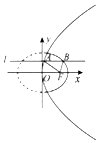 如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )
如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )
 如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )
如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )| A. | 3 | B. | $3\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
 为了测算如图阴影部分的面积,作一个边长为3的正方形将其包含在内,并向正方形内随机投掷600个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )
为了测算如图阴影部分的面积,作一个边长为3的正方形将其包含在内,并向正方形内随机投掷600个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )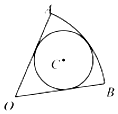 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.