题目内容
14．平面截球得到的半径是3的圆面，球心到这个平面的距离是4，则该球的表面积是（ ）| A． | 20π | B． | $\frac{416\sqrt{3}π}{3}$ | C． | $\frac{500π}{3}$ | D． | 100π |
分析 作出球的轴截面图，根据条件求出球的半径，然后根据球的表面积公式进行计算即可．
解答 
解：作出球的轴截面图，由题意知BC=3，
球心到这个平面的距离为4，即OC=4，
∴球的半径OB=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴球的表面积为4π×52=100π．
故选D．
点评 本题主要考查球的表面积的计算，根据条件求出球的半径是解决本题的关键．
练习册系列答案
相关题目
4．
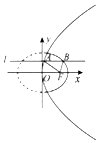如图动直线l：y=b与抛物线y2=4x交于点A，与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B，F为抛物线的焦点，则AF+BF+AB的最大值为（ ）
如图动直线l：y=b与抛物线y2=4x交于点A，与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B，F为抛物线的焦点，则AF+BF+AB的最大值为（ ）| A． | 3 | B． | $3\sqrt{2}$ | C． | 2 | D． | $2\sqrt{2}$ |
5．函数y=sin2x的单调减区间是（ ）
| A． | $[\frac{π}{2}+2kπ，\frac{3}{2}π+2kπ]（k∈Z）$ | B． | $[kπ+\frac{π}{4}，kπ+\frac{3}{4}π]（k∈Z）$ | ||
| C． | [π+2kπ，3π+2kπ]（k∈Z） | D． | $[kπ-\frac{π}{4}，kπ+\frac{π}{4}]（k∈Z）$ |
6．集合A={0，1，2}，B={x|x=3-2a，a∈A}，则A∩B=（ ）
| A． | {1} | B． | {1，2} | C． | {0，1，2} | D． | ∅ |
3．下列命题中，不是公理的是（ ）
| A． | 平行于同一条直线的两条直线平行 | |
| B． | 如果一条直线上的两点在一个平面内，那么这条直线在此平面内 | |
| C． | 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线 | |
| D． | 如果两个角的两边分别平行，则这两个角相等或互补 |
1．设集合A={1，2，3，4}，B={x|x2≤4}，则A∩B=（ ）
| A． | {1，2} | B． | {0，1} | C． | {0，1，2} | D． | {1，2，3，4} |