题目内容
12.已知A、B、C是圆O上的三个点,CO的延长线与线段BA的延长线交于圆外一点.若$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$,其中m,n∈R.则m+n的取值范围是( )| A. | (0,1) | B. | (-1,0) | C. | (1,+∞) | D. | (-∞,-1) |
分析 先利用向量数量积运算性质,将$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$,两边平方,消去半径得m、n的数量关系,利用向量加法的平行四边形法则,可判断m+n一定为负值,从而可得正确结果.
解答 解:∵|OC|=|OB|=|OA|,$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$,
∴1=m2+n2+2mncos∠AOB
当∠AOB=60°时,m2+n2+mn=1,m<0,n>0,即(m+n)2-mn=1,即(m+n)2=1+mn<1,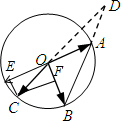
所以(m+n)2<1,
∴-1<m+n<1,当$\overrightarrow{OA}$,$\overrightarrow{OB}$趋近射线OD,
由平行四边形法则$\overrightarrow{OC}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,此时显然m<0,n>0,且|m|>|n|,
∴m+n<0,所以m+n的取值范围(-1,0).
故选B.
点评 本题主要考查了平面向量的几何意义,平面向量加法的平行四边形法则,平面向量基本定理,平面向量数量积运算的综合运用,属于中档题.

练习册系列答案
相关题目
7.己知${a^{\frac{2}{3}}}=\frac{4}{9}(a>0)$,则${log_a}\frac{3}{2}$=( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | -3 | D. | 3 |
17.已知等差数列{an}中,a5=9,且2a3-a2=6,则a1等于( )
| A. | -2 | B. | -3 | C. | 0 | D. | 1 |
4.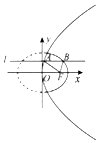 如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )
如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )
 如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )
如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )| A. | 3 | B. | $3\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
1.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点为E,过双曲线的左焦点且垂直于x轴的直线与该双曲线相交于A、B两点,若∠AEB=90°,则该双曲线的离心率e是( )
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | 2 | C. | $\frac{{\sqrt{5}+1}}{2}$或2 | D. | 不存在 |
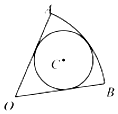 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.