��Ŀ����
19���ҹ�����������ѧ���ؾ��ط����˴�����������������������ġ���б��ʽ�������ABC�����ڽ�A��B��C���Եı߷ֱ�Ϊa��b��c�����ΪS������б�������ʽΪ$S=\sqrt{\frac{1}{4}[{{a^2}{c^2}-{{��{\frac{{{a^2}+{c^2}-{b^2}}}{2}}��}^2}}]}$����a2sinC=4sinA����a+c��2=12+b2�����á���б�������ʽ��á�ABC�����Ϊ��������| A�� | $\sqrt{3}$ | B�� | 2 | C�� | 3 | D�� | $\sqrt{6}$ |
���� �������Ҷ�������a2sinC=4sinA��ac=4�����ɣ�a+c��2=12+b2��a2+c2-b2=4�����ù�ʽ�ɵý��ۣ�
��� �⣺�������Ҷ�������a2sinC=4sinA��ac=4�����ɣ�a+c��2=12+b2��a2+c2-b2=4����${S_{��ABC}}=\sqrt{\frac{1}{4}��{16-4}��}=\sqrt{3}$��
��ѡA��
���� ������Ҫ�������������Ӧ�ã�Ҫ����ȷ������ȵĹ�ϵ���Ƚϻ�����

��ϰ��ϵ�д�
�����Ŀ
9������$f��x��=Asin����x+ϕ����A��0���أ�0��|ϕ|��\frac{��}{2}��$�IJ���ͼ����ͼ��ʾ����f��x���Ľ���ʽ�ǣ�������
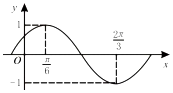

| A�� | $f��x��=sin��x+\frac{��}{6}��$ | B�� | $f��x��=sin��x+\frac{��}{3}��$ | C�� | $f��x��=sin��2x+\frac{��}{6}��$ | D�� | $f��x��=sin��2x+\frac{��}{3}��$ |
7����֪${a^{\frac{2}{3}}}=\frac{4}{9}��a��0��$����${log_a}\frac{3}{2}$=��������
| A�� | $\frac{1}{3}$ | B�� | $-\frac{1}{3}$ | C�� | -3 | D�� | 3 |
14�����к����У��뺯��$f��x��=\frac{1}{{\root{3}{x}}}$�Ķ�������ͬ�ĺ����ǣ�������
| A�� | y��x��=x•ex | B�� | $y=\frac{sinx}{x}$ | C�� | $y=\frac{x}{sinx}$ | D�� | $y=\frac{lnx}{x}$ |
4��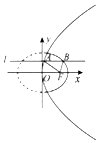 ��ͼ��ֱ��l��y=b��������y2=4x���ڵ�A������Բ$\frac{x^2}{2}+{y^2}=1$�����������Ҳ�ĵ�B��FΪ�����ߵĽ��㣬��AF+BF+AB�����ֵΪ��������
��ͼ��ֱ��l��y=b��������y2=4x���ڵ�A������Բ$\frac{x^2}{2}+{y^2}=1$�����������Ҳ�ĵ�B��FΪ�����ߵĽ��㣬��AF+BF+AB�����ֵΪ��������
 ��ͼ��ֱ��l��y=b��������y2=4x���ڵ�A������Բ$\frac{x^2}{2}+{y^2}=1$�����������Ҳ�ĵ�B��FΪ�����ߵĽ��㣬��AF+BF+AB�����ֵΪ��������
��ͼ��ֱ��l��y=b��������y2=4x���ڵ�A������Բ$\frac{x^2}{2}+{y^2}=1$�����������Ҳ�ĵ�B��FΪ�����ߵĽ��㣬��AF+BF+AB�����ֵΪ��������| A�� | 3 | B�� | $3\sqrt{2}$ | C�� | 2 | D�� | $2\sqrt{2}$ |
