题目内容
12.如图1,在边长为4的正三角形ABC中,D,F分别为AB,AC的中点,E为AD的中点.将△BCD与△AEF分别沿CD,EF同侧折起,使得二面角A-EF-D与二面角B-CD-E的大小都等于90°,得到如图2所示的多面体.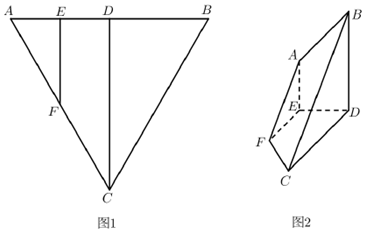
(1)在多面体中,求证:A,B,D,E四点共同面;
(2)求多面体的体积.
分析 (1)推导出AE⊥平面DEFC,BD⊥平面DEFC,从而AE∥BD,由此能证明A,B,D,E四点共同面.
(2)求出AE是四棱锥A-CDEF的高,点A到平面BCD的距离等于点E到平面BCD的距离,多面体的体积V=VA-CDEF+VA-BCD,由此能求出结果.
解答 证明:(1)因为二面角A-EF-D的大小等于90°,
所以平面AEF⊥平面DEFC,
又AE⊥EF,AE?平面AEF,平面AEF∩平面DEFC=EF,
所以AE⊥平面DEFC,
同理,可得BD⊥平面DEFC,
所以AE∥BD,故A,B,D,E四点共同面.
解:(2)因为AE⊥平面DEFC,BD⊥平面DEFC,EF∥CD,AE∥BD,DE⊥CD,
所以AE是四棱锥A-CDEF的高,点A到平面BCD的距离等于点E到平面BCD,
又$AE=DE=1,CD=2\sqrt{3}$,$EF=\sqrt{3}$,
所以$V={V_{A-CDEF}}+{V_{A-BCD}}=\frac{1}{3}{S_{梯形CDEF}}•DE+\frac{1}{3}{S_{△BCD}}•DE=\frac{{7\sqrt{3}}}{6}$.
点评 本题考查四点共面的证明,考查多面体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
2.已知等比数列{an}满足a1=$\frac{1}{2},{a_2}{a_8}=2{a_5}$+3,则a9=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{9}{8}$ | C. | 648 | D. | 18 |
3.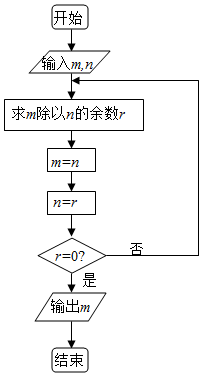 阅读如图所示的程序框图,运行相应的程序,若输入m=168,n=72,则输出m的值为( )
阅读如图所示的程序框图,运行相应的程序,若输入m=168,n=72,则输出m的值为( )
 阅读如图所示的程序框图,运行相应的程序,若输入m=168,n=72,则输出m的值为( )
阅读如图所示的程序框图,运行相应的程序,若输入m=168,n=72,则输出m的值为( )| A. | 72 | B. | 24 | C. | 12 | D. | 6 |
7.已知2a+2b=2c,则a+b-2c的最大值等于( )
| A. | -2 | B. | -1 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
1.在面积为1的正方形ABCD内部随机取一点p,则△PAB的面积大于等于$\frac{1}{3}$的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
8.已知3cos2θ=tanθ+3,且θ≠kπ(k∈Z),则sin[2(π-θ)]等于( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
5.已知复数m=4-xi,n=3+2i,若复数$\frac{n}{m}$∈R,则实数x的值为( )
| A. | -6 | B. | 6 | C. | $\frac{8}{3}$ | D. | -$\frac{8}{3}$ |