题目内容
已知方程4x2+ky2=1的曲线是焦点在y轴上的椭圆，则实数k的取值范围为 ．
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：先把方程整理成椭圆的标准方程，进而根据焦点在y轴推断出
＞
求得k的范围，进而根据k＞0综合可得k的范围．
| 1 |
| k |
| 1 |
| 4 |
解答：
解：椭圆方程4x2+ky2=1化为
+
=1，
由于椭圆的焦点在y轴上，则
＞
，即0＜k＜4，
故答案为：0＜k＜4．
| x2 | ||
|
| y2 | ||
|
由于椭圆的焦点在y轴上，则
| 1 |
| k |
| 1 |
| 4 |
故答案为：0＜k＜4．
点评：本题主要考查了椭圆的定义．解题时注意看焦点在x轴还是在y轴．
练习册系列答案
相关题目
若数列{an}是等比数列，a2=1，其前n项和为Sn，则S3的取值范围是（ ）
| A、（-∞，1] |
| B、（-∞，0）∪（1，+∞） |
| C、[3，+∞） |
| D、（-∞，-1]∪[3，+∞） |
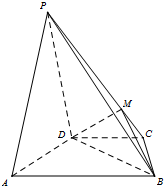如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB∥DC，PD=PA，已知AB=2DC=10，BD=
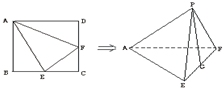已知正方形ABCD的边长为2，点E、F分别为边BC，CD的中点，沿AE、EF、AF折叠成一个三棱锥P-AEF（使B，C，D重合于点P），则三棱锥P-AEF的外接球的表面积为（ ）