题目内容
已知函数f(x)=x3-3x.
(1)求函数f(x)的极值;
(2)已知f(x)在[t,t+2]上是增函数,求t的取值范围;
(3)设f(x)在[t,t+2]上最大值M与最小值m之差为g(t),试求g(t)的解析式.
(1)求函数f(x)的极值;
(2)已知f(x)在[t,t+2]上是增函数,求t的取值范围;
(3)设f(x)在[t,t+2]上最大值M与最小值m之差为g(t),试求g(t)的解析式.
考点:利用导数求闭区间上函数的最值
专题:函数的性质及应用,导数的综合应用
分析:本题(1)利用导函数值的正负,从而知道函数的单调区间,确定函数的极值;(2)利用(1)的结论,f(x)在[t,t+2]上是增函数,即区间[t,t+2]为增区间,得到t的取值范围;(3)通过分类讨论,确定的最值,从而用t表示它们的差,得到g(t)的解析式,即得到本题结论.
解答:
解:(1)∵函数f(x)=x3-3x,
∴f′(x)=3x2-3=3(x-1)(x+1),
∴当x<-1时,f′(x)>0,f(x)单调递增;
当-1<x<1时,f′(x)<0,f(x)单调递增;
当x>1时,f′(x)>0,f(x)单调递增;
当x=-1时,f′(x)=0,f(x)有极大值f(-1)=2;
当x=1时,f′(x)=0,f(x)有极小值f(1)=-2.
∴f(x)的极大值为2,极小值为-2.
(2)由(1)知:f(x)单调递增区间为(-∞,-1],[1,+∞).
∵f(x)在[t,t+2]上是增函数,
∴t+2≤-1或t≥1,
∴t≤-3或t≥1.
∴t的取值范围为:(-∞,-3]∪[1,+∞).
(3)∵f(x)在[t,t+2]上最大值M与最小值m,
∴①当t+2≤-1,即t≤-3时,f(x)在区间[t,t+2]上单调递增,
∴M=f(t+2),m=f(t),
∴g(t)=M-m=f(t+2)-f(t)=(t+2)3-3(t+2)-(t3-3t)=6t2+12t+2;
②当t≤-1<t+2,即-3<t≤-1时,f(x)在区间[t,-1]上单调递增,在[-1,t+2]上单调递减,
∴M=f(-1)=2,
f(t+2)-f(t)=6t2+12t+2,
(i)当6t2+12t+2≥0,即-3<t≤-
时,
∴m=f(t)=6t2+12t+2,
g(t)=M-m=-6t2-12t;
(ii)当6t2+12t+2<0,即-
≤t≤-1时,
∴m=f(t+2)=t3+6t2+9t+2,
g(t)=M-m=-t3-6t2-9t;
③当-1<t<1时,1<t+2<3,
f(x)在区间[t,1]上单调递减,在[1,t+2]上单调递增,
∴m=f(1)=-2,
f(t+2)-f(t)=6t2+12t+2,
(i)当6t2+12t+2≥0,即
≤t<1时,
∴M=f(t+2)=t3+6t2+9t+2,
g(t)=M-m=t3+6t2+9t+4;
(ii)当6t2+12t+2<0,即-1<t<
时,
∴M=f(t)=6t2+12t+2;
g(t)=M-m=6t2+12t+4;
④当t≥1时,f(x)在区间[t,t+2]上单调递增,
∴M=f(t+2),m=f(t),
∴g(t)=M-m=f(t+2)-f(t)=(t+2)3-3(t+2)-(t3-3t)=6t2+12t+2.
综上,①当t≤-3时,g(t)=6t2+12t+2;
②当-3<t≤-
时,g(t)=M-m=-6t2-12t;
③当-
≤t≤-1时,g(t)=M-m=-t3-6t2-9t;
④当-1<t<
时,g(t)=M-m=6t2+12t+4;
⑤当
≤t<1时,g(t)=M-m=t3+6t2+9t+4;
⑥当t≥1时,g(t)=6t2+12t+2.
∴f′(x)=3x2-3=3(x-1)(x+1),
∴当x<-1时,f′(x)>0,f(x)单调递增;
当-1<x<1时,f′(x)<0,f(x)单调递增;
当x>1时,f′(x)>0,f(x)单调递增;
当x=-1时,f′(x)=0,f(x)有极大值f(-1)=2;
当x=1时,f′(x)=0,f(x)有极小值f(1)=-2.
∴f(x)的极大值为2,极小值为-2.
(2)由(1)知:f(x)单调递增区间为(-∞,-1],[1,+∞).
∵f(x)在[t,t+2]上是增函数,
∴t+2≤-1或t≥1,
∴t≤-3或t≥1.
∴t的取值范围为:(-∞,-3]∪[1,+∞).
(3)∵f(x)在[t,t+2]上最大值M与最小值m,
∴①当t+2≤-1,即t≤-3时,f(x)在区间[t,t+2]上单调递增,
∴M=f(t+2),m=f(t),
∴g(t)=M-m=f(t+2)-f(t)=(t+2)3-3(t+2)-(t3-3t)=6t2+12t+2;
②当t≤-1<t+2,即-3<t≤-1时,f(x)在区间[t,-1]上单调递增,在[-1,t+2]上单调递减,
∴M=f(-1)=2,
f(t+2)-f(t)=6t2+12t+2,
(i)当6t2+12t+2≥0,即-3<t≤-
3+
| ||
| 3 |
∴m=f(t)=6t2+12t+2,
g(t)=M-m=-6t2-12t;
(ii)当6t2+12t+2<0,即-
3+
| ||
| 3 |
∴m=f(t+2)=t3+6t2+9t+2,
g(t)=M-m=-t3-6t2-9t;
③当-1<t<1时,1<t+2<3,
f(x)在区间[t,1]上单调递减,在[1,t+2]上单调递增,
∴m=f(1)=-2,
f(t+2)-f(t)=6t2+12t+2,
(i)当6t2+12t+2≥0,即
-3+
| ||
| 3 |
∴M=f(t+2)=t3+6t2+9t+2,
g(t)=M-m=t3+6t2+9t+4;
(ii)当6t2+12t+2<0,即-1<t<
-3+
| ||
| 3 |
∴M=f(t)=6t2+12t+2;
g(t)=M-m=6t2+12t+4;
④当t≥1时,f(x)在区间[t,t+2]上单调递增,
∴M=f(t+2),m=f(t),
∴g(t)=M-m=f(t+2)-f(t)=(t+2)3-3(t+2)-(t3-3t)=6t2+12t+2.
综上,①当t≤-3时,g(t)=6t2+12t+2;
②当-3<t≤-
3+
| ||
| 3 |
③当-
3+
| ||
| 3 |
④当-1<t<
-3+
| ||
| 3 |
⑤当
-3+
| ||
| 3 |
⑥当t≥1时,g(t)=6t2+12t+2.
点评:本题考查了用导函数法研究函数的单调性、极值、最值,还考查了分类讨论的数学思想,本题运算量较大,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
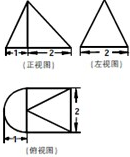
一个几何体的三视图如图,其俯视图是一个等边三角形,则这个几何体的体积为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、(4+π)
|
“m=1”是“直线mx+(2m-1)y+1=0和直线3x+my-3=0垂直”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
方程lgx+x=0在下列的哪个区间内有实数解( )
A、[-10,-
| ||
| B、(-∞,0] | ||
| C、[1,10] | ||
D、[
|