题目内容
已知cos(
-α)=
,sin(α+β)=1,求cos(2α+β)的值.
| 3π |
| 2 |
| 1 |
| 3 |
考点:两角和与差的余弦函数,任意角的概念
专题:三角函数的求值
分析:根据已知和诱导公式先求出sinα,cosα,cos(α+β)的值,从而可求cos(2α+β)的值.
解答:
解:cos(
-α)=
⇒-cos(
-α)=
⇒sinα=-
,⇒cosα=±
=±
,
cos(α+β)=
=0,
cos(2α+β)=cos[α+(α+β)]=cosαcos(α+β)-sinαsin(α+β)=(±
)×0-(-
)×1=
.
| 3π |
| 2 |
| 1 |
| 3 |
| π |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1-sin2α |
2
| ||
| 3 |
cos(α+β)=
| 1-sin2α |
cos(2α+β)=cos[α+(α+β)]=cosαcos(α+β)-sinαsin(α+β)=(±
2
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题主要考察了两角和与差的余弦函数,同角三角函数的关系式的应用,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
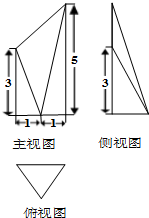 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为( )
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为( )A、
| ||||
B、
| ||||
C、8
| ||||
D、
|
函数f(x)=sin(2x+φ)(|φ<
|)的图象向左平移
个单位后关于原点对称,求函数f(x)在[0,
]上的最小值为( )
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
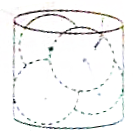 如图,在底面直径为4r的圆柱内,正方放入4个半径为r的小球,使得圆柱上下表面与小球正好相切,则圆柱的高为
如图,在底面直径为4r的圆柱内,正方放入4个半径为r的小球,使得圆柱上下表面与小球正好相切,则圆柱的高为 在正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,DD1,CD的中点,N为BC的中点,试在E,F,G,H四个点中找两个点,使这两个点与点N确定一个平面α,且平面α∥平面BB1D1D.
在正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,DD1,CD的中点,N为BC的中点,试在E,F,G,H四个点中找两个点,使这两个点与点N确定一个平面α,且平面α∥平面BB1D1D.