题目内容
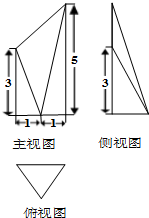 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为( )
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为( )A、
| ||||
B、
| ||||
C、8
| ||||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:首先把三视图转化为立体图,然后根据三视图中的线段长和线面的关系,求出锥体的体积.
解答:
 解:首先把几何体的三视图复原成立体图形
解:首先把几何体的三视图复原成立体图形
根据三视图中的线段长,得知:AD=3,CE=5,AC=2
由于俯视图是边长为2的正三角形,进一步求得:AB=2,AF=1
利用勾股定理得:BF=
根据三视图的特点得知:BF⊥底面DACE,
VB-DACE=
SDACE•BF=
•
(3+5)×2×
=
,
故选:D
 解:首先把几何体的三视图复原成立体图形
解:首先把几何体的三视图复原成立体图形根据三视图中的线段长,得知:AD=3,CE=5,AC=2
由于俯视图是边长为2的正三角形,进一步求得:AB=2,AF=1
利用勾股定理得:BF=
| 3 |
根据三视图的特点得知:BF⊥底面DACE,
VB-DACE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 8 |
| 3 |
| 3 |
故选:D
点评:本题考查的知识要点:三视图与立体图的相互转化,求立体图的体积,锥体的体积公式的应用,属于基础题型.

练习册系列答案
相关题目
设a∈R,则“a=1”是“直线l1:ax+(1-a)y=3”与直线l2:(a-1)x+(2a+3)y=2互相垂直的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知函数f(x)=
的定义域为( )
| 1 | ||
|
| A、[0,+∞) |
| B、[1,+∞) |
| C、(1,+∞) |
| D、[0,1] |
已知数列{an}是等差数列,且a3+a4+a5+a6+a7=160,则a1+a9=( )
| A、32 | B、64 | C、96 | D、128 |
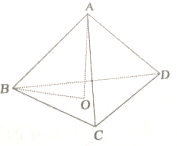 如图,四面体ABCD中,AB、AC、AD两两垂直,若△BCD的垂心为O,求证:AO⊥平面BCD.
如图,四面体ABCD中,AB、AC、AD两两垂直,若△BCD的垂心为O,求证:AO⊥平面BCD.