题目内容
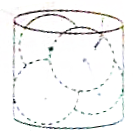 如图,在底面直径为4r的圆柱内,正方放入4个半径为r的小球,使得圆柱上下表面与小球正好相切,则圆柱的高为
如图,在底面直径为4r的圆柱内,正方放入4个半径为r的小球,使得圆柱上下表面与小球正好相切,则圆柱的高为考点:球内接多面体,棱柱的结构特征
专题:计算题,作图题,空间位置关系与距离
分析:由题意,四个小球球心的连线构成正四面体,求出对边的距离,再加上2r即为圆柱的高.
解答:
 解:由题意,四个小球球心的连线构成正四面体,
解:由题意,四个小球球心的连线构成正四面体,
其中正四面体的棱长为2r,如图,
取AB、AC、BD的中点F、E、G,连结EF、FG、EG;
则可知EF∥BC、FG∥AD,AD⊥BC;
则△FEG是直角三角形,
且EF=FG=r,
则EG=
r,
则则圆柱的高为r+r+
r=(2+
)r.
故答案为:(2+
)r.
 解:由题意,四个小球球心的连线构成正四面体,
解:由题意,四个小球球心的连线构成正四面体,其中正四面体的棱长为2r,如图,
取AB、AC、BD的中点F、E、G,连结EF、FG、EG;
则可知EF∥BC、FG∥AD,AD⊥BC;
则△FEG是直角三角形,
且EF=FG=r,
则EG=
| 2 |
则则圆柱的高为r+r+
| 2 |
| 2 |
故答案为:(2+
| 2 |
点评:本题考查了学生的空间想象力与作图能力,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
给出下列四个命题:其中真命题的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” |
| C、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| D、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
抛物线y=-
x2的准线方程为( )
| 1 |
| 6 |
A、x=
| ||
B、y=
| ||
C、x=
| ||
D、y=
|
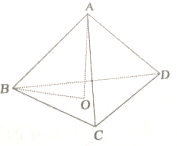 如图,四面体ABCD中,AB、AC、AD两两垂直,若△BCD的垂心为O,求证:AO⊥平面BCD.
如图,四面体ABCD中,AB、AC、AD两两垂直,若△BCD的垂心为O,求证:AO⊥平面BCD.