题目内容
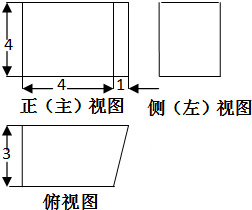
一个空间几何体的三视图如图所示,则该几何体的体积为( )

| A、12 | B、18 | C、27 | D、54 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:该几何体是一个以俯视图为底面的柱体,求出底面面积和高,进而可得该几何体的体积.
解答:
解:由三视图可知:该几何体是一个以俯视图为底面的柱体,
棱柱的底面面积S=
×(4+5)×3=
,
棱柱的高h=4,
故棱柱的体积V=Sh=54,
故选:D
棱柱的底面面积S=
| 1 |
| 2 |
| 27 |
| 2 |
棱柱的高h=4,
故棱柱的体积V=Sh=54,
故选:D
点评:本题考查的知识点是由三视图求几何体的体积或表面积,由三视图正确恢复原几何体是解题的关键.

练习册系列答案
相关题目
已知函数:f(x)=x2-4|x|+1,若关于x的方程:f(x)=2k恰有四个不等的实数根,则实数k的取值范围为( )
A、-
| ||||
| B、-3<k<1 | ||||
| C、-6<k<2 | ||||
D、k>-
|
已知函数f(x)=
,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
|
| A、a<0 | B、a≤0 |
| C、a<3 | D、0<a<3 |
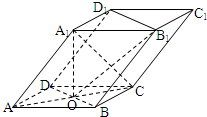 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=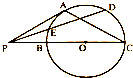 如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=
如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=