题目内容
某单位有老年人28人,中年人44人,青年人72人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( )
| A、简单随机抽样 |
| B、系统抽样 |
| C、分层抽样 |
| D、先从老年人中剔除一人,然后分层抽样 |
考点:分层抽样方法
专题:概率与统计
分析:由于总体由具有明显不同特征的三部分构成,故应采用分层抽样的方法,若直接采用分层抽样,则运算出的结果不是整数,先从老年人中剔除一人,然后分层抽样.
解答:
解:由于总体由具有明显不同特征的三部分构成,故不能采用简单随机抽样,也不能用系统抽样,
若直接采用分层抽样,则运算出的结果不是整数,先从老年人中剔除一人,然后分层抽样,此时,每个个体被抽到的概率等于
=
,从各层中抽取的人数分别为 28×
=7,44×
=11,
72×
=18.
故选:C.
若直接采用分层抽样,则运算出的结果不是整数,先从老年人中剔除一人,然后分层抽样,此时,每个个体被抽到的概率等于
| 36 |
| 28+44+72 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
72×
| 1 |
| 4 |
故选:C.
点评:本题考查分层抽样的定义和方法,注意使用分层抽样的题目的特点.

练习册系列答案
相关题目
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ≤2π)若ω在集合{2,3,4}中任取一个数,φ在,{
π,
π,
π,π}中任取一个数,从这些函数中任意抽取两个,其图象能经过相同的平移后得到y=2sinωx的概率为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知扇形的面积为2,扇形圆心角的弧度数是4,则扇形的周长为( )
| A、6 | ||
B、6
| ||
| C、10 | ||
| D、12 |
甲、乙、丙三人站成一排,则甲、乙相邻的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )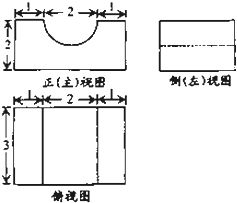

A、24-
| ||||
B、24-
| ||||
| C、24-π | ||||
D、24-
|
不等式x2<2x+3的解集是( )
| A、(-1,3) |
| B、(-1,1) |
| C、(-3,-1)∪(1,3) |
| D、(-3,3) |