题目内容
若cosα-3sinα=
，则tanα=（ ）
| 10 |
| A、3 | ||
B、-
| ||
| C、-3 | ||
D、
|
考点：同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：cosα-3sinα=
，两边平方，再弦化切，即可求得结论．
| 10 |
解答：
解：∵cosα-3sinα=
，
∴8sin2α-6cosαsinα=9，
∴
=9，
∴tanα=-3，
故选：C．
| 10 |
∴8sin2α-6cosαsinα=9，
∴
| 8tan2α-6tanα |
| tan2α+1 |
∴tanα=-3，
故选：C．
点评：本题考查同角三角函数基本关系的运用，考查学生的计算能力，比较基础．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
若方程
+
=1表示准线平行于x轴的椭圆，则m的范围是（ ）
| x2 |
| m2 |
| y2 |
| (m-1)2 |
A、m＞
| ||
B、m＜
| ||
C、m＞
| ||
D、m＜
|
已知a＞0，且a≠1，则函数f（x）=ax+（x-1）2-2a的零点个数为（ ）
| A、1 | B、2 | C、3 | D、与a有关 |
已知f（x）=
，又α，β为锐角三角形的两内角，则（ ）
|
| A、f（sinα）＞f（cosβ） |
| B、f（sinα）＜f（cosβ） |
| C、f（sinα）＞f（sinβ） |
| D、f（cosα）＞f（cosβ） |
已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ≤2π）若ω在集合{2，3，4}中任取一个数，φ在，{
π，
π，
π，π}中任取一个数，从这些函数中任意抽取两个，其图象能经过相同的平移后得到y=2sinωx的概率为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}为等比数列，且a2=2，a5=16，则公比q（ ）
| A、1 | B、2 | C、4 | D、8 |
用1，2，3，4这四个数字，组成比2 000大且无重复数字的四位数的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知某几何体的三视图如图，其中正（主）视图中半圆的半径为1，则该几何体的体积为（ ）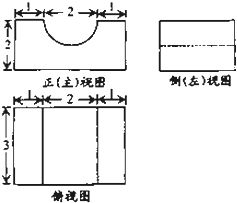
A、24-
| ||||
B、24-
| ||||
| C、24-π | ||||
D、24-
|