题目内容
1.在△ABC中,角A,B,C所对的边分别为a,b,c,若A=$\frac{π}{3}$,B=$\frac{π}{4}$且a=$\sqrt{3}$,则b=$\sqrt{2}$.分析 利用正弦定理即可得出.
解答 解:由正弦定理可得:$\frac{\sqrt{3}}{sin\frac{π}{3}}$=$\frac{b}{sin\frac{π}{4}}$,解得b=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了正弦定理、三角函数求值,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
9.某学校高三年级有学生500人,其中男生300名,女生200名,为了研究学生的数学成绩(单位:分)是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学成绩,然后按性别分为男、女两组,再将两组学生的数学成绩分成5组,分别加以统计,得到如图所示的频率分布直方图.
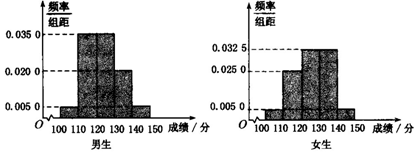
(1)从样本中数学成线小于110分的学生中随机抽取2名学生,求2名学生恰好为一男一女的概率;
(2)若规定数学成绩不小于130分的学生为“数学尖子生”,得到如下数据表:请你根据已知条件完成下列2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
参考数据:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.

(1)从样本中数学成线小于110分的学生中随机抽取2名学生,求2名学生恰好为一男一女的概率;
(2)若规定数学成绩不小于130分的学生为“数学尖子生”,得到如下数据表:请你根据已知条件完成下列2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
| 数学尖子生 | 数学尖子生 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 | 100 |
| P(K2≥k2) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
10.设函数f(x)=x3-3x2,若过点(2,n)可作三条直线与曲线y=f(x)相切,则实数n的取值范围是( )
| A. | (-5,-4) | B. | (-5,0) | C. | (-4,0) | D. | (-5,-3] |