题目内容
3.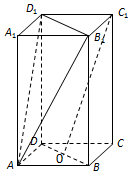 如图,长方体ABCD-A1B1C1D1中,O是BD的中点,AA1=2AB=2BC=4.
如图,长方体ABCD-A1B1C1D1中,O是BD的中点,AA1=2AB=2BC=4.(1)求证:C1O∥平面AB1D1
(2)点E在侧棱AA1上,求四棱锥E-BB1D1D的体积.
分析 (1)连结A1C1交B1D1于O1,连结AC,AO1,通过证明四边形AOC1O1是平行四边形得出OC1∥AO1,于是C1O∥平面AB1D1;
(2)证明AO⊥平面BB1D1D,于是E到平面BB1D1D的距离为AO,代入体积公式计算即可.
解答  (1)证明:连结A1C1交B1D1于O1,连结AC,AO1,
(1)证明:连结A1C1交B1D1于O1,连结AC,AO1,
则AO∥C1O1,AO=C1O1,
∴四边形AOC1O1是平行四边形,
∴OC1∥AO1,又OC1?平面AB1D1,AO1?平面AB1D1,
∴C1O∥平面AB1D1.
(2)解:∵四边形ABCD是正方形,
∴AO⊥BD,
∵BB1⊥平面ABCD,AO?平面ABCD,
∴AO⊥BB1,又BB1∩BD=B,
∴AO⊥平面BB1D1D,
∵AA1∥BB1,A到平面BB1D1D的距离等于E到平面BB1D1D的距离.
∵AA1=2AB=2BC=4,∴BD=2$\sqrt{2}$,AO=$\sqrt{2}$,
∴V${\;}_{E-B{B}_{1}{D}_{1}D}$=$\frac{1}{3}{S}_{矩形B{B}_{1}{D}_{1}D}•AO$=$\frac{1}{3}×4×2\sqrt{2}×\sqrt{2}$=$\frac{16}{3}$.
点评 本题考查了线面平行、线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
18.设曲线y=ex-x及直线y=0所围成的图形为区域D,不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$所确定的区域为E,在区域E内随机取一点,则该点落在区域D内的概率为( )
| A. | $\frac{{{e^2}-2e-1}}{4e}$ | B. | $\frac{{{e^2}-2e}}{4e}$ | C. | $\frac{{{e^2}-e-1}}{4e}$ | D. | $\frac{{{e^2}-1}}{4e}$ |
15.对于实数x,y,若|x-1|≤2,|y-1|≤2,则|x-2y+1|的最大值为( )
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
12.若z∈C,i为虚数单位,且$\frac{z}{{|z{|^2}}}=\frac{3}{5}-\frac{4}{5}i$,则复数z等于( )
| A. | $\frac{3}{5}+\frac{4}{5}i$ | B. | $\frac{3}{5}-\frac{4}{5}i$ | C. | $\frac{5}{3}-\frac{5}{4}i$ | D. | $\frac{4}{5}-\frac{3}{5}i$ |
13.已知实数a,b满足(a+i)(1-i)=3+bi(i为虚数单位),记z=a+bi,则|z|是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 5 | D. | 25 |