题目内容
8．在等差数列{an}中，已知a4=4，a8=-4，则a12=-12．分析 利用等差数列{an}的性质可得：2a8=a4+a12，即可得出．
解答 解：由等差数列{an}的性质可得：2a8=a4+a12，
又a4=4，a8=-4，∴a12=2×（-4）-4=-12．
故答案为：-12．
点评 本题考查了等差数列的性质，属于基础题．
练习册系列答案
相关题目
19．已知i是虚数单位，复数$\frac{z}{2-3i}$对应于复平面内一点（0，1），则|z|=（ ）
| A． | $\sqrt{13}$ | B． | 4 | C． | 5 | D． | $4\sqrt{2}$ |
16．若复数满足（z-1）（2-i）=5i，其中是虚数单位，则|z|的值为（ ）
| A． | 2 | B． | $\sqrt{5}$ | C． | $\frac{{\sqrt{170}}}{3}$ | D． | $\frac{{\sqrt{149}}}{3}$ |
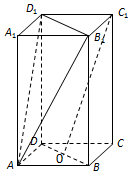如图，长方体ABCD-A1B1C1D1中，O是BD的中点，AA1=2AB=2BC=4．