题目内容
15.对于实数x,y,若|x-1|≤2,|y-1|≤2,则|x-2y+1|的最大值为( )| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
分析 利用绝对值的几何意义,转化求解最值即可.
解答 解:实数x,y,若|x-1|≤2,|y-1|≤2,则x∈[-1,3],y∈[-1,3],
则|x-2y+1|=|x-1-2(y-1)|≤|x-1|+2|y-1|≤2+2×2=6.
当且仅当x=-1或3,y=-1或3时,取等号.
故选:D.
点评 本题考查绝对值三角不等式的解法,考查转化思想以及计算能力.

练习册系列答案
相关题目
4.已知点P在双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$上,点A满足$\overrightarrow{PA}=(t-1)\overrightarrow{OP}$(t∈R),且$\overrightarrow{OA}•\overrightarrow{OP}=64$,$\overrightarrow{OB}=(0,1)$,则$|{\overrightarrow{OB}•\overrightarrow{OA}}|$的最大值为( )
| A. | $\frac{5}{4}$ | B. | $\frac{24}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{24}$ |
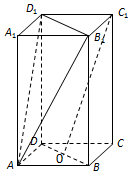 如图,长方体ABCD-A1B1C1D1中,O是BD的中点,AA1=2AB=2BC=4.
如图,长方体ABCD-A1B1C1D1中,O是BD的中点,AA1=2AB=2BC=4.