题目内容
7.函数f(x)=$\frac{ln|x|}{{x}^{2}}$的图象大致为( )| A. | 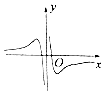 | B. | 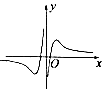 | C. | 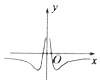 | D. | 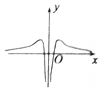 |
分析 先判断函数为偶函数,再分段讨论函数值得情况,即可判断.
解答 解:函数的定义域为(-∞,0)∪(0,+∞),
∵f(-x)=$\frac{ln|-x|}{(-x)^{2}}$=$\frac{ln|x|}{{x}^{2}}$=f(x),
∴f(x)为偶函数,
∴f(x)的图象关于y轴对称,
当0<x<1时,lnx<0,
∴f(x)<0,
当x>1时,lnx>0,
∴f(x)>0,
当x=1时,f(x)=0,
故选:D
点评 本题考查了函数图象的识别,关键是掌握函数的奇偶性和函数值得变化趋势,属于中档题.

练习册系列答案
相关题目
2.设a,b∈R,则“a+b≥4”是“a≥2且b≥2”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.已知全集U={1,2,3,4,5,6,7},A={2,4,5},B={1,3,5,7},则A∩(∁UB)为( )
| A. | {1,4,6} | B. | {2,4,6} | C. | {2,4} | D. | {4} |
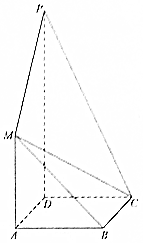 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.