Question

2．如图，在长方体ABCDA₁B₁C₁D₁中，棱锥A₁ABCD的体积与长方体AC₁的体积的比值为（　　）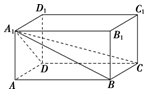 

• A． $\frac{1}{2}$
• B． $\frac{1}{6}$
• C． $\frac{1}{3}$
• D． $\frac{1}{5}$

Answer 1

分析 设AB=a，AD=b，AA₁=c，分别求出棱锥A₁ABCD的体积和长方体AC₁的体积，由此能求出棱锥A₁ABCD的体积与长方体AC₁的体积的比值．

解答 解：设AB=a，AD=b，AA₁=c，
棱锥A₁ABCD的体积V₁=$\frac{1}{3}×c×（a×b）=\frac{1}{3}abc$，
长方体AC₁的体积V₂=abc，
∴棱锥A₁ABCD的体积与长方体AC₁的体积的比值为：
$\frac{{V}_{1}}{{V}_{2}}=\frac{\frac{1}{3}abc}{abc}$=$\frac{1}{3}$．
故选：C．

点评 本题考查四棱锥体积与长方体体积的比值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．