题目内容
10.若非零函数f(x)对于任意的实数a,b均有f(a+b)=f(a)?f(b),且当x<0时,f(x)>1.(1)求f(0)的值;
(2)求证:$f(-x)=\frac{1}{f(x)}$;
(3)求证:f(x)>0;
(4)求证:f(x)为减函数;
(5)当$f(4)=\frac{1}{16}$时,解不等式f(x2+x-3)?f(5-x2)≤$\frac{1}{4}$.
分析 (1)根据抽象函数,利用赋值法取a=b=0,即可求出f(0)=1;
(2)取a=x,b=-x,即可证明
(3)结合(2)可得x>0时,f(x)∈(0,1),再结合(1)知f(x)>0,x∈R.
(4)根据函数单调性的定义证明f(x)为R上的减函数;
(5)利用函数单调性的性质,解不等式即可.
解答 解:(1)取a=b=0,得f(0)=[f(0)]2,而f(x)≠0,所以f(0)=1.
证明:(2)取a=x,b=-x,则f(0)=f(x)•f(-x)=1,则$f(-x)=\frac{1}{f(x)}$.
证明:(3)由(2)及x<0时,f(x)>1,可知$f(-x)=\frac{1}{f(x)}$∈(0,1),
即x>0时,f(x)∈(0,1).
再结合(1)知f(x)>0,x∈R.
证明:(4)当b<0时,a+b<a,f(b)>1,f(a)>0,
∴f(a+b)=f(a)?f(b)>f(a)?1=f(a),
故f(x)为减函数.
(5)∵$\frac{1}{16}=f(4)=f(2+2)=f(2)•f(2)$,且f(2)>0,
∴$f(2)=\frac{1}{4}$.
于是不等式f(x2+x-3)?f(5-x2)≤$\frac{1}{4}$可以化为f(x+2)≤f(2),
再由f(x)为R上的减函数得
x+2≥2⇒x≥0
∴不等式的解集为[0,+∞).
点评 本题主要考查抽象函数的应用,以及函数单调性的定义,以及利用函数的单调性解不等式,考查学生的运算能力.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
1.若a=lnπ,b=log32,$c={(-2)^{\frac{1}{3}}}$,则它们的大小关系为( )
| A. | a>c>b | B. | b>a>c | C. | a>b>c | D. | b>c>a |
18.已知x3=4,则x等于( )
| A. | $\root{4}{3}$ | B. | $\root{3}{4}$ | C. | log34 | D. | log43 |
15.函数y=log${\;}_{\frac{1}{2}}$(x2-3x+2)的单调递增区间为是( )
| A. | (0,+∞) | B. | (-∞,1) | C. | (-∞,$\frac{3}{2}$] | D. | (2,+∞) |
2.如图,在长方体ABCDA1B1C1D1中,棱锥A1ABCD的体积与长方体AC1的体积的比值为( ) 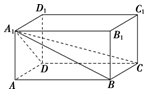

| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |