题目内容
17.已知集合A={3,32,33,…,3n}(n≥3),从中选出3个不同的数,使这3个数按一定的顺序排列构成等比数列,记满足此条件的等比数列的个数为f(n)(Ⅰ)f(5)=8;
(Ⅱ)若f(n)=220,则n=22.
分析 (I)n=5时,A═{3,32,33,34,35},从中选出3个不同的数,使这3个数按一定的顺序排列构成等比数列,则共有3,32,33;32,33,34;33,34,35;3,33,35.其顺序反过来也成立.可得f(5).
(II)A={3,32,33,…,3n}(n≥3),公比为3的共有:n-2个;公比为$\frac{1}{3}$的共有:n-2个.公比为32的共有:n-4个;公比为$\frac{1}{{3}^{2}}$的共有:n-4个.…,则f(n)=220=2[(n-2)+(n-4)+…2],即可得出.
解答 解:(I)n=5时,A═{3,32,33,34,35},从中选出3个不同的数,使这3个数按一定的顺序排列构成等比数列,则共有3,32,33;32,33,34;33,34,35;3,33,35.其顺序反过来也成立.因此f(5)=8.
(II)A={3,32,33,…,3n}(n≥3),
公比为3的共有:n-2个;公比为$\frac{1}{3}$的共有:n-2个.
公比为32的共有:n-4个;公比为$\frac{1}{{3}^{2}}$的共有:n-4个.
…,
则f(n)=220=2[(n-2)+(n-4)+…2],
∴$\frac{(n-2+2)×\frac{n-2}{2}}{2}×2=220$,n2-2n-440=0,
解得n=22.
故答案为:8,22.
点评 本题考查了等差数列与等比数列的通项公式求和公式及其性质,考查了分类讨论方法、推理能力与计算能力,属于难题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
1.若a=lnπ,b=log32,$c={(-2)^{\frac{1}{3}}}$,则它们的大小关系为( )
| A. | a>c>b | B. | b>a>c | C. | a>b>c | D. | b>c>a |
2.如图,在长方体ABCDA1B1C1D1中,棱锥A1ABCD的体积与长方体AC1的体积的比值为( ) 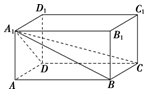

| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
12.已知等差数列{an}的前n项和为Sn,a2=2,S5=15,则数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前2017项和为( )
| A. | $\frac{2016}{2017}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
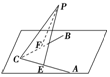 ∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.
∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.