题目内容
14.已知函数f(x)=$\left\{\begin{array}{l}{-\sqrt{x},x>0}\\{(x-\frac{1}{x})^{4},x<0}\end{array}\right.$,则f(f(2))=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
分析 先求出f(2)=-$\sqrt{2}$,从而f(f(2))=f(-$\sqrt{2}$),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{-\sqrt{x},x>0}\\{(x-\frac{1}{x})^{4},x<0}\end{array}\right.$,
∴f(2)=-$\sqrt{2}$,
f(f(2))=f(-$\sqrt{2}$)=(-$\sqrt{2}+\frac{1}{\sqrt{2}}$)4=(-$\frac{\sqrt{2}}{2}$)4=$\frac{1}{4}$.
故选:A.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
2.如图,在长方体ABCDA1B1C1D1中,棱锥A1ABCD的体积与长方体AC1的体积的比值为( ) 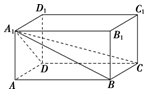

| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
12.已知等差数列{an}的前n项和为Sn,a2=2,S5=15,则数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前2017项和为( )
| A. | $\frac{2016}{2017}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
10.已知角θ的终边过点P(-12,5),则cosθ=( )
| A. | $\frac{5}{13}$ | B. | $-\frac{12}{13}$ | C. | $\frac{12}{13}$ | D. | $-\frac{5}{13}$ |