题目内容
12. (1)某简单几何体的三视图中,正视图、侧视图、俯视图都是如图所示的直角边长为1的等腰直角三角形,求该几何体的表面积和体积;
(1)某简单几何体的三视图中,正视图、侧视图、俯视图都是如图所示的直角边长为1的等腰直角三角形,求该几何体的表面积和体积;(2)三棱锥O-ABC中,OB=AC=5,OA=BC=$\sqrt{41}$,AB=OC=$\sqrt{34}$,求该三棱锥的外接球体的表面积和体积.
分析 (1)由三视图可知,直观图的底面是等腰直角三角形,侧棱垂直底面,利用所给数据,求该几何体的表面积和体积;
(2)构造长方体,使得面上的对角线长分别为5,$\sqrt{41}$,$\sqrt{34}$,则长方体的对角线长等于三棱锥O-ABC外接球的直径,即可求出三棱锥O-ABC外接球的表面积和体积.
解答 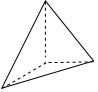 解:(1)由三视图可知,直观图的底面是等腰直角三角形,侧棱垂直底面,
解:(1)由三视图可知,直观图的底面是等腰直角三角形,侧棱垂直底面,
S=3×$\frac{1}{2}×1×1$+$\frac{\sqrt{3}}{4}×2$=$\frac{3+\sqrt{3}}{2}$,---------------(2分)
V=$\frac{1}{3}×\frac{1}{2}×1×1×1$=$\frac{1}{6}$-------------------------(4分)
(2)构造长方体,使得面上的对角线长分别为5,$\sqrt{41}$,$\sqrt{34}$,
则长方体的对角线长等于三棱锥O-ABC外接球的直径.
设长方体的棱长分别为x,y,z,则x2+y2=25,y2+z2=41,x2+z2=34,
∴x2+y2+z2=50
∴三棱锥O-ABC外接球的直径为5$\sqrt{2}$,
∴三棱锥S-ABC外接球的表面积为π•50=50π------------------(6分)
V=$\frac{4}{3}π•(\frac{5\sqrt{2}}{2})^{3}$=$\frac{125}{3}\sqrt{2}π$----------------(8分)
点评 本题考查球内接多面体,考查三视图,构造长方体,利用长方体的对角线长等于四面体外接球的直径是关键.

练习册系列答案
相关题目
2.已知函数f(x)=alnx-bx2,a,b∈R.若f(x)在x=1处与直线y=-$\frac{1}{2}$相切.
(1)求a,b的值;
(2)求f(x)在[$\frac{1}{e}$,e]上的最大值.
(1)求a,b的值;
(2)求f(x)在[$\frac{1}{e}$,e]上的最大值.
1.若a=lnπ,b=log32,$c={(-2)^{\frac{1}{3}}}$,则它们的大小关系为( )
| A. | a>c>b | B. | b>a>c | C. | a>b>c | D. | b>c>a |
2.如图,在长方体ABCDA1B1C1D1中,棱锥A1ABCD的体积与长方体AC1的体积的比值为( ) 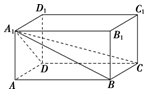

| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
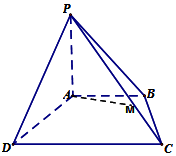 四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.
四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.