题目内容
7.A,B两个工厂距一条河分别为400m和100m,A、B两工厂之间距离500m,且位于小河同侧.把小河看作一条直线,今在小河边上建一座供水站,供A,B两工厂用水,要使供水站到A,B两工厂铺设的水管长度之和最短,问供水站应建在什么地方?分析 以小河所在直线为x轴,过点A的垂线为y轴,建立直角坐标系,点A(0,400)关于x轴的对称点A′(0,-400),由两点式得直线A′B的方程为y=$\frac{5}{4}$x-400,即可得出结论.
解答 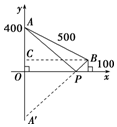 解:如图,以小河所在直线为x轴,过点A的垂线为y轴,建立直角坐标系,
解:如图,以小河所在直线为x轴,过点A的垂线为y轴,建立直角坐标系,
则点A(0,400),点B(a,100).
过点B作BC⊥AO于点C.
在△ABC中,AB=500,AC=400-100=300,
由勾股定理得BC=400,所以B(400,100).
点A(0,400)关于x轴的对称点A′(0,-400),
由两点式得直线A′B的方程为y=$\frac{5}{4}$x-400.
令y=0,得x=320,即点P(320,0).
故供水站(点P)在距O点320 m处时,到A,B两厂铺设的水管长度之和最短.
点评 本题考查利用数学知识解决实际问题,考查直线方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
18.已知x3=4,则x等于( )
| A. | $\root{4}{3}$ | B. | $\root{3}{4}$ | C. | log34 | D. | log43 |
15.函数y=log${\;}_{\frac{1}{2}}$(x2-3x+2)的单调递增区间为是( )
| A. | (0,+∞) | B. | (-∞,1) | C. | (-∞,$\frac{3}{2}$] | D. | (2,+∞) |
2.如图,在长方体ABCDA1B1C1D1中,棱锥A1ABCD的体积与长方体AC1的体积的比值为( ) 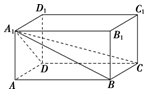

| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
3.设函数f(x)=$\frac{{4}^{x}}{{4}^{x}+1}$,若[x]表示不超过x的最大整数,则函数y=[f(x)-$\frac{1}{2}$]+[f(x)+$\frac{1}{2}$]的值域是( )
| A. | {0,-1} | B. | {0,1} | C. | {-1,1} | D. | {-1,0,1} |
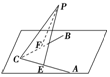 ∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.
∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.