题目内容
18．如果点P（sin2θ，2cosθ）位于第三象限，那么角θ所在的象限是（ ）| A． | 第一象限角 | B． | 第二象限角 | C． | 第三象限角 | D． | 第四象限角 |
分析 根据所给的点在第三象限，写出这个点的横标和纵标都小于0，根据这两个都小于0，得到角的正弦值大于0，余弦值小于0，得到角是第二象限的角．
解答 解：∵点P（sin2θ，2cosθ）位于第三象限，
∴sin2θ=2sinθcosθ＜0，2cosθ＜0，
∴sinθ＞0，cosθ＜0，
∴θ是第二象限的角．
故选：B．
点评 本题考查三角函数的符号，这是一个常用到的知识点，给出角的范围要求说出三角函数的符号，反过来给出三角函数的符号要求看出角的范围，属于基础题．
练习册系列答案
相关题目
2．如图，在长方体ABCDA1B1C1D1中，棱锥A1ABCD的体积与长方体AC1的体积的比值为（ ）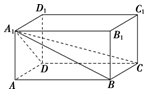 
| A． | $\frac{1}{2}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{5}$ |
13．关于函数f（x）=x2-2x+1的零点，下列说法正确的是（ ）
| A． | 因为f（0）?f（2）＞0，所以f（x）在（0，2）内没有零点 | |
| B． | 因为1是f（x）的一个零点，所以f（0）?f（2）＜0 | |
| C． | 由于f（x）在区间（-∞，0）上单调递减，所以f（x）在（-∞，0）内有唯一的一个零点 | |
| D． | 以上说法都不对 |
3．设函数f（x）=$\frac{{4}^{x}}{{4}^{x}+1}$，若[x]表示不超过x的最大整数，则函数y=[f（x）-$\frac{1}{2}$]+[f（x）+$\frac{1}{2}$]的值域是（ ）
| A． | {0，-1} | B． | {0，1} | C． | {-1，1} | D． | {-1，0，1} |
10．已知角θ的终边过点P（-12，5），则cosθ=（ ）
| A． | $\frac{5}{13}$ | B． | $-\frac{12}{13}$ | C． | $\frac{12}{13}$ | D． | $-\frac{5}{13}$ |
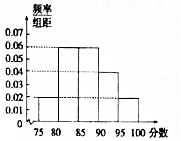某校为了了解高三学生体育达标情况，在高三学生体育达标成绩中随机抽取50个进行调研，按成绩分组：第l组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到的频率分布直方图如图所示：若要在成绩较高的第3，4，5组中用分层抽样抽取6名学生进行复查：