题目内容
已知在数列{an}中,a1=2,an+1=4an-3n+1,n∈N.
(1)证明:数列{an-n}是等比数列;
(2)求数列{an}的通项式及其前n项和Sn.
(1)证明:数列{an-n}是等比数列;
(2)求数列{an}的通项式及其前n项和Sn.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)由已知条件得an+1-(n+1)=4(an-n),由此能证明数列{an-n}是等比数列.
(2)由a1=2,a1-1=1,
=4,由此能求出数列{an}的通项式及其前n项和Sn.
(2)由a1=2,a1-1=1,
| an+1-(n+1) |
| an-n |
解答:
(1)证明:∵在数列{an}中,a1=2,an+1=4an-3n+1,
∴an+1-(n+1)=4(an-n),
∴
=4,
∴数列{an-n}是等比数列.
(2)解:∵a1=2,a1-1=1,
=4,
∴an-n=1×4n-1,
∴an=n+4n-1.
∴Sn=
+
=
+
.
∴an+1-(n+1)=4(an-n),
∴
| an+1-(n+1) |
| an-n |
∴数列{an-n}是等比数列.
(2)解:∵a1=2,a1-1=1,
| an+1-(n+1) |
| an-n |
∴an-n=1×4n-1,
∴an=n+4n-1.
∴Sn=
| n(n+1) |
| 2 |
| 1-4n |
| 1-4 |
=
| n(n+1) |
| 2 |
| 4n-1 |
| 3 |
点评:本题考查等比数列的证明,考查数列的通项公式和前n项和公式的合理运用,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
命题“x<1”是命题“x≤1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
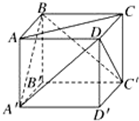 若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连接正方体的各个顶点的所有直线中,“黄金异面直线对”共有( )
若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连接正方体的各个顶点的所有直线中,“黄金异面直线对”共有( )| A、12对 | B、18对 |
| C、24对 | D、30对 |
若a=1.70.3,b=0.93.1,c=log30.7,则a,b,c的大小关系是( )
| A、a>b>c |
| B、a>c>b |
| C、b>c>a |
| D、c>b>a |
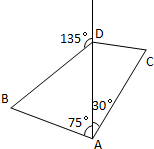 如图,某轮船从海岛A出发沿正方向航行,灯塔B在海岛A北偏西75°的方向上,且与海岛A相距
如图,某轮船从海岛A出发沿正方向航行,灯塔B在海岛A北偏西75°的方向上,且与海岛A相距