题目内容
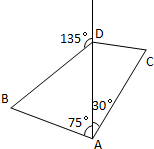如图，某轮船从海岛A出发沿正方向航行，灯塔B在海岛A北偏西75°的方向上，且与海岛A相距4| 6 |
| 3 |
（1）求D与海岛A的距离；
（2）求D与灯塔C的距离．
考点：解三角形的实际应用
专题：应用题,解三角形
分析：（1）在△ABD中，由正弦定理可求AD；
（2）在△ACD中，由余弦定理得CD．
（2）在△ACD中，由余弦定理得CD．
解答：
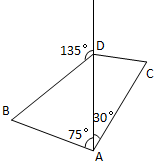解：（1）由题意得在△ABD中，AB=4
，∠DAB=75°，∠ADB=45°，
由正弦定理得
=
，…（2分）
∴AD=
=
=12n mile …（5分）
（2）由（1）得AD=12，在△ACD中，AC=8
，∠DAC=30°，…（7分）
由余弦定理得CD2=AC2+AD2-2AC•ADcos30°=48，
∴CD=4
n mile．…（10分）
解：（1）由题意得在△ABD中，AB=4| 6 |
由正弦定理得
| AD |
| sin∠ABD |
| AB |
| sin∠ADB |
∴AD=
| AB•sin∠ABD |
| sin∠ADB |
4
| ||
| sin45° |
（2）由（1）得AD=12，在△ACD中，AC=8
| 3 |
由余弦定理得CD2=AC2+AD2-2AC•ADcos30°=48，
∴CD=4
| 3 |
点评：本题的考点是解三角形的实际应用，主要考查了正弦定理、余弦定理在解三角形中的应用，解决实际问题的关键是要把实际问题转化为数学问题，然后利用数学知识进行求解．
练习册系列答案
相关题目
如图所示程序运行的结果是（ ）
| A、210，11 |
| B、200，9 |
| C、210，9 |
| D、200，11 |
