题目内容

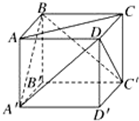若两条异面直线所成的角为60°，则称这对异面直线为“黄金异面直线对”，在连接正方体的各个顶点的所有直线中，“黄金异面直线对”共有（　　）
A、12对B、18对
C、24对D、30对
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：正方体ABCD-A ′B ′C ′D ′中，在连接正方体的各个顶点的所有直线中，若要出现所成角为60°的异面直线，则直线需为面对角线，由此能求出所求的黄金异面直线对共有多少对．
解答： 解：如图，正方体ABCD-A ′B ′C ′D ′中，
在连接正方体的各个顶点的所有直线中，
若要出现所成角为60°的异面直线，
则直线需为面对角线，
以AC为例，与之构成黄金异面直线对的直线有4条，
分别是A′B，BC′，A′D，C′D，
正方体的面对角线有12条，
所以所求的黄金异面直线对共有
12×4
2
=24对．
故选：C．
点评：本题考查“黄金异面直线对”有多少对的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
设
a
=（x，4，3），
b
=（3，2，z），且
a
∥
b
，则xz等于
 
．
已知a1=
1
2
，an=4an-1+1，（n＞1），则a5=（　　）
A、13B、53
C、213D、853
如图所示程序运行的结果是（　　）
A、210，11
B、200，9
C、210，9
D、200，11
函数f（x）=
x3+x
x2
+3（x＞0）的最小值是（　　）
A、5
B、3
33
C、3
D、2
定义一种运算a?b=
a，a≤b
b，a≥b
例如2?3=2，令f（x）=（cos2x+sinx）?
5
4
，x∈[0，
π
2
]，则函数f(x-
π
2
)的最大值是（　　）
A、
5
4
B、-
5
4
C、1
D、-1
已知a是实数，（a+i）（1+i）是纯虚数，则a等于（　　）
A、2B、1C、-1D、-2
已知在数列{an}中，a1=2，an+1=4an-3n+1，n∈N．
（1）证明：数列{an-n}是等比数列；
（2）求数列{an}的通项式及其前n项和Sn．
（1）在（x-
2
）2004的二项式中，含x的奇次幂的项之和为S，当x=
2
时，求S．
（2）已知（x2-
i
x
）n的展开式中第三项与第五项的系数之比为-
3
14
，求展开式中常数项．
（3）若多项式x2+x10=a0+a1（x+1）+…+a9（x+1）9+a10（x+1）10，求a9．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网