题目内容
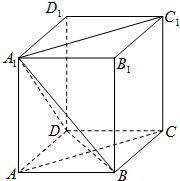 如图,ABCD-A1B1C1D1是长方体,AB=AD=a,AA1=2a.
如图,ABCD-A1B1C1D1是长方体,AB=AD=a,AA1=2a.(1)求多面体A1B1C1D1-BCD的体积;
(2)求证:平面A1BD⊥平面ACC1A1.
考点:平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)多面体A1B1C1D1-BCD的体积V=V长方体-VA1-ACD;
(2)欲证平面ACC1A1⊥平面A1BD,根据面面垂直的判定定理可知在平面A1BD内一直线与平面ACC1A1垂直,而根据线面垂直的判定定理可得BD⊥平面ACC1A1.
(2)欲证平面ACC1A1⊥平面A1BD,根据面面垂直的判定定理可知在平面A1BD内一直线与平面ACC1A1垂直,而根据线面垂直的判定定理可得BD⊥平面ACC1A1.
解答:
(1)解:多面体A1B1C1D1-BCD的体积V=V长方体-VA1-ACD…(2分)
=AB×AD×AA1-
×
×AB×AD×AA1…(4分)
=
a3…(6分)
(2)证明:A1B1C1D1-ABCD是长方体,AA1⊥底面ABCD…(7分),
所以AA1⊥BD…(9分)
又因为AB=AD且ABCD是长方体,所以AC⊥BD…(10分)
因为AA1∩AC=A,所以BD⊥平面ACC1A1…(12分)
因为BD?平面A1BD,所以平面A1BD⊥平面ACC1A1…(14分).
=AB×AD×AA1-
| 1 |
| 3 |
| 1 |
| 2 |
=
| 5 |
| 3 |
(2)证明:A1B1C1D1-ABCD是长方体,AA1⊥底面ABCD…(7分),
所以AA1⊥BD…(9分)
又因为AB=AD且ABCD是长方体,所以AC⊥BD…(10分)
因为AA1∩AC=A,所以BD⊥平面ACC1A1…(12分)
因为BD?平面A1BD,所以平面A1BD⊥平面ACC1A1…(14分).
点评:本小题主要考查空间中的线面关系,考查面面垂直的判定,考查识图能力和逻辑思维能力,考查转化思想,属于中档题.

练习册系列答案
相关题目
 已知在棱长为1的正方体ABCD-A1B1C1D1中,E、F、M分别是A1C1,A1D和B1A上任一点,求证:平面A1EF∥平面B1MC.
已知在棱长为1的正方体ABCD-A1B1C1D1中,E、F、M分别是A1C1,A1D和B1A上任一点,求证:平面A1EF∥平面B1MC.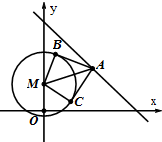 已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.
已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.