题目内容
数列{an}中，a1＞0，a1≠1，又an+1=
，n∈N*．
（1）若a1=
，求a2，a3，a4，a5的值，并归纳出数列{an}的通项公式；
（2）是否存在常数p（p≠0），使得{1+
}为等比数列？若存在，求出其公比；若不存在，请说明理由．
| 2an |
| an+1 |
（1）若a1=
| 1 |
| 2 |
（2）是否存在常数p（p≠0），使得{1+
| p |
| an |
考点：等比关系的确定,数列递推式,归纳推理
专题：等差数列与等比数列
分析：（1）根据an+1=
，n∈N*．a1=
，求a2，a3，a4，a5的值，观察各项分子通项为2n-1，分母通项为2n-1+1，于是可以写出通项公；
（2）假设存在常数p（p≠0），使得{1+
}为等比数列，公比为q，据此可以求出1+
+
=q+
，故能求出q和p的值．
| 2an |
| an+1 |
| 1 |
| 2 |
（2）假设存在常数p（p≠0），使得{1+
| p |
| an |
| p |
| 2 |
| p |
| 2an |
| pq |
| an |
解答：
解：（1）a2=
，a3=
，a4=
，a5=
，
归纳猜想an=
．
（2）假设存在常数p（p≠0），使得{1+
}为等比数列，公比为q，则有
1+
=q（1+
），
因为an+1=
，所以1+
=q(1+
)，
化简得，1+
+
=q+
，
令
，
解得p=-1，q=
，
经检验符合题意，故存在p=-1，使得{1+
}为等比数列，公比为
| 2 |
| 3 |
| 4 |
| 5 |
| 8 |
| 9 |
| 16 |
| 17 |
归纳猜想an=
| 2n-1 |
| 2n-1+1 |
（2）假设存在常数p（p≠0），使得{1+
| p |
| an |
1+
| p |
| an+1 |
| p |
| an |
因为an+1=
| 2an |
| an+1 |
| p (an+1) |
| 2an |
| p |
| an |
化简得，1+
| p |
| 2 |
| p |
| 2an |
| pq |
| an |
令
|
解得p=-1，q=
| 1 |
| 2 |
经检验符合题意，故存在p=-1，使得{1+
| p |
| an |
| 1 |
| 2 |
点评：本题主要考查数列递推式和等差关系的确定等知识点，熟练掌握反证法和归纳法进行数学解题，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
从1、2、3、4、5、6这六个数中，每次取出两个不同数记为a、b，则共可得到3
的不同数值的个数（ ）
| b |
| a |
| A、20 | B、22 | C、24 | D、28 |
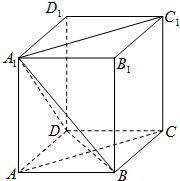如图，ABCD-A1B1C1D1是长方体，AB=AD=a，AA1=2a．