题目内容
已知向量
=（
，-1），
=（cos
，sin
），记f（x）=2
•
sin
．
（1）若x∈[0，π]，求函数f（x）的值域；
（2）设在△ABC中，角A、B、C所对的边分别为a、b、c，若f（c）=1，且b2=ac，求sinA的值．
| a |
| 3 |
| b |
| x |
| 3 |
| x |
| 3 |
| a |
| b |
| x |
| 3 |
（1）若x∈[0，π]，求函数f（x）的值域；
（2）设在△ABC中，角A、B、C所对的边分别为a、b、c，若f（c）=1，且b2=ac，求sinA的值．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（I）利用向量的数量积运算、倍角公式、两角和差的正弦公式、正弦函数的单调性即可得出；
（II）利用正弦函数的单调性有界性、勾股定理、直角三角形的边角关系即可得出．
（II）利用正弦函数的单调性有界性、勾股定理、直角三角形的边角关系即可得出．
解答：
解：（Ⅰ）f(x)=2
sin
cos
-2sin2
=
sin
+cos
-1=2sin(
+
)-1．
∵x∈[0，π]，∴
≤
+
≤
，
∴
≤sin(
+
)≤1，
∴0≤2sin(
+
)-1≤1，
∴f（x）的值域为[0，1]．
（Ⅱ）由（Ⅰ）得f(C)=2sin(
+
)-1=1，
∴sin(
+
)=1，
又C∈（0，π），
∴
≤
+
≤
，
∴C=
，
在Rt△ABC中，∵b2=ac，c2=a2+b2，
∴c2=a2+ac⇒(
)2+
-1=0，
又c＞a，解得
=
，
∴sinA=
=
．
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
| 3 |
| 2x |
| 3 |
| 2x |
| 3 |
| 2x |
| 3 |
| π |
| 6 |
∵x∈[0，π]，∴
| π |
| 6 |
| 2x |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
∴
| 1 |
| 2 |
| 2x |
| 3 |
| π |
| 6 |
∴0≤2sin(
| 2x |
| 3 |
| π |
| 6 |
∴f（x）的值域为[0，1]．
（Ⅱ）由（Ⅰ）得f(C)=2sin(
| 2C |
| 3 |
| π |
| 6 |
∴sin(
| 2C |
| 3 |
| π |
| 6 |
又C∈（0，π），
∴
| π |
| 6 |
| 2C |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
∴C=
| π |
| 2 |
在Rt△ABC中，∵b2=ac，c2=a2+b2，
∴c2=a2+ac⇒(
| a |
| c |
| a |
| c |
又c＞a，解得
| a |
| c |
-1+
| ||
| 2 |
∴sinA=
| a |
| c |
| ||
| 2 |
点评：本题考查了向量的数量积运算、倍角公式、两角和差的正弦公式、正弦函数的单调性、勾股定理、直角三角形的边角关系，考查了推理能力和计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
设函数f（x）的图象是一条连续不断的曲线，满足f（2.25）＜0，f（2.5）＞0，f（2.75）＞0，则下列区间中，函数f（x）必然有零点的一个区间是（ ）
| A、（2，2.25） |
| B、（2.25，2.5） |
| C、（2.5，2.75） |
| D、（2.75，3） |
已知f（x）是定义在R上的函数，满足f（x）+f（-x）=0，f（x-1）=f（x+1），当x∈[0，1），f（x）=
，函数f（x）的最小值为（ ）
| 2x |
| 4x+1 |
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
从1、2、3、4、5、6这六个数中，每次取出两个不同数记为a、b，则共可得到3
的不同数值的个数（ ）
| b |
| a |
| A、20 | B、22 | C、24 | D、28 |
命题“对任意x∈R，总有x2+1＞0”的否定是（ ）
| A、“对任意x∉R，总有x2+1＞0” |
| B、“对任意x∈R，总有x2+1≤0” |
| C、“存在x∈R，使得x2+1＞0” |
| D、“存在x∈R，使得x2+1≤0” |
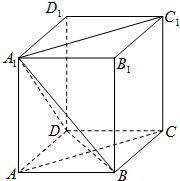如图，ABCD-A1B1C1D1是长方体，AB=AD=a，AA1=2a．