题目内容
已知在棱长为1的正方体ABCD-A1B1C1D1中，E、F、M分别是A1C1，A1D和B1A上任一点，求证：平面A1EF∥平面B1MC．考点：平面与平面平行的判定
专题：证明题,空间位置关系与距离
分析：建立坐标系，求出平面A1EF、平面B1MC的法向量，即可证明结论．
解答：
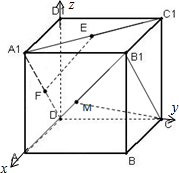证明：建立如图所示的坐标系，则
=（-1，1，0），
=（-1，0，-1），
=（1，0，1），
=（0，-1，-1），
设
=λ
，
=μ
，
=ω
，
设
=（x，y，z）为平面A1EF的法向量，则
，
∴
=（1，1，-1）；
同理平面B1MC的法向量为
=（-1，-1，1），
∴
=-
，
∴
∥
，
∴平面A1EF∥平面B1MC．
证明：建立如图所示的坐标系，则| A1C1 |
| B1C |
| A1D |
| B1A |
设
| A1E |
| A1C1 |
| A1F |
| A1D |
| B1M |
| B1A |
设
| m |
|
∴
| m |
同理平面B1MC的法向量为
| n |
∴
| m |
| n |
∴
| m |
| n |
∴平面A1EF∥平面B1MC．
点评：本题考查平面与平面平行的判定，考查向量法的运用，求出平面的法向量是关键．
练习册系列答案
相关题目
已知向量
=（3，4），
=（-1，2），则
=（ ）
| AB |
| AC |
| CB |
| A、（4，2） |
| B、（2，6） |
| C、（5，3） |
| D、（-1，5） |
命题“对任意x∈R，总有x2+1＞0”的否定是（ ）
| A、“对任意x∉R，总有x2+1＞0” |
| B、“对任意x∈R，总有x2+1≤0” |
| C、“存在x∈R，使得x2+1＞0” |
| D、“存在x∈R，使得x2+1≤0” |
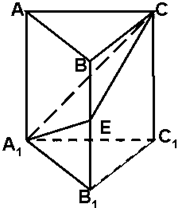如图，在正三棱柱ABC-A1B1C1中，E为BB1的中点，求证：截面A1EC⊥侧面AC1．
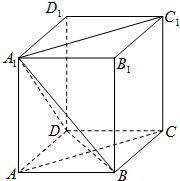如图，ABCD-A1B1C1D1是长方体，AB=AD=a，AA1=2a．