题目内容
已知向量
=(x,-1),
=(y-1,1)(x>0,y>0),若
∥
,则t=x+
+y+
的最小值是( )
| a |
| b |
| a |
| b |
| 1 |
| x |
| 1 |
| y |
| A、4 | B、5 | C、6 | D、8 |
考点:基本不等式
专题:不等式的解法及应用
分析:由向量平行可得x+y=1,可得t=x+
+y+
=1+
+
=1+(
+
)(x+y)=1+2+
+
,由基本不等式可得.
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
| y |
| x |
| x |
| y |
解答:
解:∵
=(x,-1),
=(y-1,1)(x>0,y>0),且
∥
,
∴x-(-1)(y-1)=0,即x+y=1
∴t=x+
+y+
=1+
+
=1+(
+
)(x+y)
=1+2+
+
≥1+2+2
=5
当且仅当x=y=
时,取等号,
故选:B
| a |
| b |
| a |
| b |
∴x-(-1)(y-1)=0,即x+y=1
∴t=x+
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
=1+2+
| y |
| x |
| x |
| y |
|
当且仅当x=y=
| 1 |
| 2 |
故选:B
点评:本题考查基本不等式,涉及向量的平行,属基础题.

练习册系列答案
相关题目
设函数f(x)的图象是一条连续不断的曲线,满足f(2.25)<0,f(2.5)>0,f(2.75)>0,则下列区间中,函数f(x)必然有零点的一个区间是( )
| A、(2,2.25) |
| B、(2.25,2.5) |
| C、(2.5,2.75) |
| D、(2.75,3) |
已知向量
=(3,4),
=(-1,2),则
=( )
| AB |
| AC |
| CB |
| A、(4,2) |
| B、(2,6) |
| C、(5,3) |
| D、(-1,5) |
在平行六面体ABCD-A1B1C1D1中,用向量
,
,
来表示向量
为( )
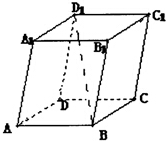
| AB |
| AD |
| AA1 |
| BD1 |

A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知f(x)是定义在R上的函数,满足f(x)+f(-x)=0,f(x-1)=f(x+1),当x∈[0,1),f(x)=
,函数f(x)的最小值为( )
| 2x |
| 4x+1 |
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
从1、2、3、4、5、6这六个数中,每次取出两个不同数记为a、b,则共可得到3
的不同数值的个数( )
| b |
| a |
| A、20 | B、22 | C、24 | D、28 |
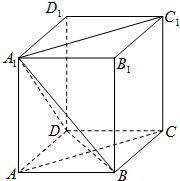 如图,ABCD-A1B1C1D1是长方体,AB=AD=a,AA1=2a.
如图,ABCD-A1B1C1D1是长方体,AB=AD=a,AA1=2a.