题目内容
已知等差数列{an}中,a2=4,a5=0,则a8= .
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:利用等差数列的通项公式求解.
解答:
解:∵等差数列{an}中,a2=4,a5=0,
∴
,解得a1=
,d=-
,
∴a8=
+(-
)×7=-4.
故答案为:-4.
∴
|
| 16 |
| 3 |
| 4 |
| 3 |
∴a8=
| 16 |
| 3 |
| 4 |
| 3 |
故答案为:-4.
点评:本题考查等差数列的第8项的求法,解题时要认真审题,是基础题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、若命题p,?q都是真命题,则命题“p∧q”为真命题 |
| B、命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0则x≠0或y≠0” |
| C、命题“?x∈R,2x>0”的否定是“?x0∈R,2 x0≤0” |
| D、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
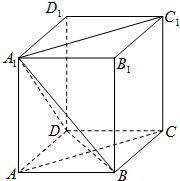 如图,ABCD-A1B1C1D1是长方体,AB=AD=a,AA1=2a.
如图,ABCD-A1B1C1D1是长方体,AB=AD=a,AA1=2a.