题目内容
△ABC的三内角A、B、C成等差数列，所对的三边a、b、c成等比数列，则A-C= ．
考点：余弦定理
专题：解三角形
分析：利用等差数列及等比数列的性质得到2B=A+C，b2=ac，求出B的度数，利用余弦定理列出关系式，把cosB及b2=ac代入得到a=c，利用等边对等角得到A=C，即可确定出A-C的值．
解答：
解：由题意得：2B=A+C，b2=ac，
∵A+B+C=180°，∴B=60°，
由余弦定理得：cosB=
=
=
，
整理得：（a-c）2=0，即a=c，
∴A=C，即A-C=0，
故答案为：0
∵A+B+C=180°，∴B=60°，
由余弦定理得：cosB=
| a2+c2-b2 |
| 2ac |
| a2+c2-ac |
| 2ac |
| 1 |
| 2 |
整理得：（a-c）2=0，即a=c，
∴A=C，即A-C=0，
故答案为：0
点评：此题考查了余弦定理，以及等差、等比数列的性质，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
设m，n是两条不同的直线，α，β是两个不同的平面，则下列命题中正确的是（ ）
| A、若m∥α，n⊥β且α⊥β，则m⊥n |
| B、若α⊥β，m∥n且 n⊥β，则m∥α |
| C、若m?α，n?β且m∥n，则α∥β |
| D、若m⊥α，n⊥β且m⊥n，则α⊥β |
如图是一个几何体的三视图，若该几何体的体积为
，则主视图中三角形的高x的值为（ ）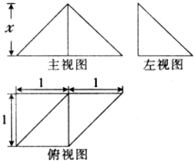
| 3 |
| 8 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
在△ABC中，若acosA=bcosB，则△ABC的形状一定是（ ）
| A、等腰直角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰或直角三角形 |
某高级中学有高一、二、三三个年级的学生共1600名，其中高三学生400名，如果通过分层抽样的方法从全体高中学生中抽取一个容量为80人的样本，则应从高三年级学生中抽取的人数是（ ）
| A、40 | B、30 | C、20 | D、10 |
若点（1，a）到直线x-y+1=0的距离是
，则实数a为（ ）
3
| ||
| 2 |
| A、-1 | B、5 |
| C、-1或5 | D、-3或3 |
下列函数中，既是偶函数又在（0，+∞）上单调递减的函数是（ ）
| A、y=x3 | ||
| B、y=-x2+1 | ||
| C、y=|x|+1 | ||
D、y=
|