题目内容

若直线a?平面α，直线b?平面β，则直线a和b的位置关系
 
．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：讨论当α∥β时，a，b平行或异面；当α、β相交时，则a，b平行或异面或相交，即可得到答案．
解答： 解：由于直线a?平面α，直线b?平面β，
则当α∥β时，a，b平行或异面；
当α、β相交时，则a，b平行或异面或相交；
故答案为：平行或异面或相交
点评：本题考查空间直线与直线、平面和平面的位置关系，属于基础题．
练习册系列答案
相关题目
设A={x|x2+4x＞0}，B={x|a-1＜x＜a+1}，其中x∈R，设U=R．
（1）求∁UA；
（2）如果B⊆∁UA，求实数a的取值范围．
已知集合M={x|y=2x}，N={x|y=lg（x-1）}，则M∩∁RN=（　　）
A、（-∞，1]B、（-∞，1）
C、RD、∅
已知函数f（x）=x（
1
2x-1
+
1
2
）．
（Ⅰ）判断函数f（x）的奇偶性；
（Ⅱ）证明f（x）＞0；
（Ⅲ）若f（x）•f（-x）=
25
36
x2，求x的值．
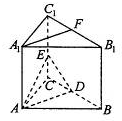如图，在直三棱柱ABC-A1B1C1中，AB=AC，D、E分别是棱BC、CC1上的点（点D不在BC的端点处），且AD⊥DE，F为B1C1的中点．
（Ⅰ）求证：平面ADE⊥平面B1BCC1；
（Ⅱ）求证：A1F∥平面ADE．
若实数x，y满足不等式组
x-2≤0
y-1≤0
x+2y-3≥0
，则目标函数z=x-2y的最大值是（　　）
A、1B、2C、3D、4
设函数y=f（x）在区间（a，b）上的导函数为f′（x），f′（x）在区间（a，b）上的导函数为f″（x），若在区间（a，b）上f″（x）＜0，则称函数f（x）在区间（a，b）上为“凸函数”，已知f（x）=
1
20
x5-
1
12
mx4-
3
2
x2在区间（-1，2）上为“凸函数”，则实数m的取值范围为（　　）
A、（-∞，
5
4
]
B、[-4，+∞）
C、[
5
4
，+∞）
D、[-4，
5
4
]
△ABC的三内角A、B、C成等差数列，所对的三边a、b、c成等比数列，则A-C=
 
．
若圆C：x2+y2-4y+3=0，关于直线2ax+by+6=0对称，则由点（a，b）向圆所作的切线长的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网