题目内容
如图是一个几何体的三视图,若该几何体的体积为
,则主视图中三角形的高x的值为( )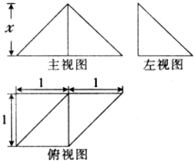
| 3 |
| 8 |

A、
| ||
B、
| ||
| C、1 | ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:该几何体是一个以俯视图为底面的四棱锥,求出底面面积,结合体积,构造关于高的方程,进而可得该几何体的高.
解答:
解:由三视图知:该几何体是一个以俯视图为底面的四棱锥,高为x,
底面分别是边长为1的正方形与直角边长为1的等腰直角三角形,
∴几何体的体积V=
×(12+
×1×1)×x=
,
∴x=
.
故选:B.
底面分别是边长为1的正方形与直角边长为1的等腰直角三角形,
∴几何体的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 8 |
∴x=
| 3 |
| 4 |
故选:B.
点评:本题考查的知识点是由三视图求几何体的体积或表面积,由三视图正确恢复原几何体是解题的关键.

练习册系列答案
相关题目
设a=
dx,则
sinxdx=( )
| ∫ | 2 0 |
| 4-x2 |
| ∫ | a 0 |
| A、2π | B、π | C、2 | D、1 |
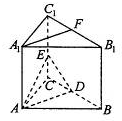 如图,在直三棱柱ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,D、E分别是棱BC、CC1上的点(点D不在BC的端点处),且AD⊥DE,F为B1C1的中点.