题目内容
10.曲线的参数方程为$\left\{{\begin{array}{l}{x=\sqrt{5}cosθ}\\{y=sinθ}\end{array},}\right.0≤θ<π$,则它的直角坐标方程为$\frac{{x}^{2}}{5}+{y}^{2}=1$,-$\sqrt{5}$<x≤$\sqrt{5}$,0≤y≤1.分析 由θ的取值范围,求得x及y的取值范围,由椭圆的参数方程,即可求得直角坐标方程.
解答 解:由参数方程为$\left\{{\begin{array}{l}{x=\sqrt{5}cosθ}\\{y=sinθ}\end{array},}\right.0≤θ<π$,-$\sqrt{5}$<x≤$\sqrt{5}$,0≤y≤1
消去参数θ,则$\frac{{x}^{2}}{5}+{y}^{2}=1$,-$\sqrt{5}$<x≤$\sqrt{5}$,0≤y≤1,
故答案为:$\frac{{x}^{2}}{5}+{y}^{2}=1$,-$\sqrt{5}$<x≤$\sqrt{5}$,0≤y≤1.
点评 本题椭圆的参数方程,考查转化思想,属于基础题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
14.一个几何体的三视图如图所示,已知这个几何体的体积为$10\sqrt{3}$,则这个几何体的外接球的表面积为( )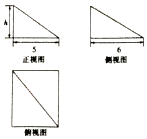

| A. | 8π | B. | 24π | C. | 48π | D. | 64π |
1.当x>0时,不等式x2-mx+9>0恒成立,则实数m的取值范围是( )
| A. | (-∞,6) | B. | (-∞,6] | C. | [6,+∞) | D. | (6,+∞) |
5.设z=1-i(i为虚数单位),若复数$\frac{2}{z}$-z2在复平面内对应的向量为$\overrightarrow{OZ}$,则向量$\overrightarrow{OZ}$的模是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
2.已知球O是某几何体的外接球,而该几何体是由一个侧棱长为2$\sqrt{5}$的正四棱锥S-ABCD与一个高为6的正四棱柱ABCD-A1B1C1D1拼接而成,则球O的表面积为( )
| A. | $\frac{100π}{3}$ | B. | 64π | C. | 100π | D. | $\frac{500π}{3}$ |