题目内容
19.在极坐标系中,曲线C1:ρ=2cosθ,曲线${C_2}:ρ{sin^2}θ=4cosθ$.以极点为坐标原点,极轴为x轴正半轴建立直角坐标系xOy,曲线C的参数方程为$\left\{{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$(t为参数).(Ⅰ)求C1,C2的直角坐标方程;
(Ⅱ)C与C1,C2交于不同四点,这四点在C上的排列顺序为P,Q,R,S,求||PQ|-|RS||的值.
分析 (I)曲线C1:ρ=2cosθ,即ρ2=2ρcosθ,利用互化公式可得直角坐标方程.曲线${C_2}:ρ{sin^2}θ=4cosθ$,即ρ2sin2θ=4ρcosθ,利用互化公式可得直角标准方程.
(II)设四点在C上的排列顺次为P,Q,R,S,其参数分别为t1,t2,t3,t4.曲线C的参数方程代入抛物线方程可得:3t2-8t-32=0.△1>0,可得t1+t4.曲线C的参数方程代入圆的方程可得:t2+t=0.△2>0,可得t2+t3.∴||PQ|-|RS||=|(t2-t1)-(t4-t3)|=|(t2+t3)-(t1+t4)|即可得出.
解答 解:(Ⅰ)∵曲线C1:ρ=2cosθ,即ρ2=2ρcosθ,
∴曲线C1的直角坐标方程为:x2+y2-2x=0,
∵曲线${C_2}:ρ{sin^2}θ=4cosθ$,即ρ2sin2θ=4ρcosθ,
∴曲线C2的直角坐标方程为:y2=4x.
(Ⅱ)设四点在C上的排列顺序为P,Q,R,S,其参数分别为t1,t2,t3,t4.
曲线C的参数方程$\left\{{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$(t为参数)代入抛物线方程y2=4x,
可得:3t2-8t-32=0.△1>0,可得t1+t4=$\frac{8}{3}$.
曲线C的参数方程$\left\{{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$(t为参数)代入圆的方程可得:t2+t=0.△2>0,可得t2+t3=-1.
∴||PQ|-|RS||=|(t2-t1)-(t4-t3)|=|(t2+t3)-(t1+t4)|=|1+$\frac{8}{3}$|=$\frac{11}{3}$.
故答案为:$\frac{11}{3}$.
点评 本题考查曲线与坐标轴的交点坐标的求法,考查极坐标方程、直角坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 总计 | 105 |
(1)请完成上面的2 x×2列联表,并根据表中数据判断,是否有95%的把握认为“成绩与班级有关系”?
(2)若甲班优秀学生中有男生6名,女生4名,现从中随机选派3名学生参加全市数学竞赛,记参加竞赛的男生人数为X,求X的分布列与期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
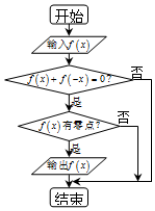 某流程图如图所示,现输入如下四个函数,则可以输出的函数是①②③.
某流程图如图所示,现输入如下四个函数,则可以输出的函数是①②③.