题目内容

14．一个几何体的三视图如图所示，已知这个几何体的体积为$10\sqrt{3}$，则这个几何体的外接球的表面积为（　　）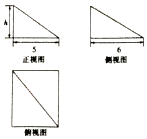
A．8πB．24πC．48πD．64π

分析 由三视图可得该几何体为底面边长为5、6，一条侧棱垂直底面的四棱锥，将该几何体补成一个长方体，求出外接球半径，代入球表面积公式，可得答案．

解答 解：由三视图可得该几何体为底面边长为5、6，一条侧棱垂直底面的四棱锥，设高为h，
则$\frac{1}{3}×5×6×h=10\sqrt{3}$，解得h=$\sqrt{3}$．
将该几何体补成一个长方体，则其外接球半径为R=$\frac{1}{2}\sqrt{25+36+3}=4$，
故这个几何体的外接球的表面积为4πR2=64π．
故选：D．

点评 本题考查了由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．属于中档题．

练习册系列答案
相关题目
16．已知矩阵A=$[\begin{array}{l}{2}&{-2}\\{0}&{1}\end{array}]$，设曲线C：（x-y）2+y2=1在矩阵A对应的变换下得到曲线C′，求C′的方程．
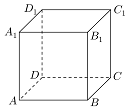5．如图，ABCD-A1B1C1D1是棱长为1的正方体，任作平面α与对角线AC1垂直，使得α与正方体的每个面都有公共点，这样得到的截面多边形的面积为S，周长为l的范围分别是[$\frac{\sqrt{3}}{2}$，$\frac{3\sqrt{3}}{4}$]、{3$\sqrt{2}$}（用集合表示）
2．已知命题p：1∈{x|x2-2x+1≤0}，命题q：?x∈[0，1]，x2-1≥0，则下列命题是真命题的是（　　）
A．p∧qB．￢p∧（￢q）C．p∨qD．￢p∨q
9．已知函数f（x）=[2sin（x+$\frac{π}{3}$）+sinx]cosx-$\sqrt{3}$sin2x
（1）求f（x）的周期；
（2）求f（x）在[0，$\frac{5π}{12}$]上的最值．
19．已知椭圆$C：\left\{\begin{array}{l}x=2cosφ\\ y=sinφ\end{array}\right.（φ$为参数），A，B是C上的动点，且满足OA⊥OB（O为坐标原点），以原点O为极点，x轴的正半轴为极轴建立坐标系，点D的极坐标为$（4，\frac{π}{3}）$．
（1）求线段AD的中点M的轨迹E的普通方程；
（2）利用椭圆C的极坐标方程证明$\frac{1}{{{{|{OA}|}^2}}}+\frac{1}{{{{|{OB}|}^2}}}$为定值，并求△AOB的面积的最大值．
6．（Ⅰ）求函数f（x）=$\frac{|3x+2|-|1-2x|}{|x+3|}$的最大值M．
（Ⅱ）是否存在满足a2+b2≤c≤M的实数a，b，c使得2（a+b+c）+1≥0．
3．已知函数f（x）=ex-mx2-2x
（1）若m=0，讨论f（x）的单调性；
（2）若$m＜\frac{e}{2}-1$，证明：当x∈[0，+∞）时，$f（x）＞\frac{e}{2}-1$．
10．曲线的参数方程为$\left\{{\begin{array}{l}{x=\sqrt{5}cosθ}\\{y=sinθ}\end{array}，}\right.0≤θ＜π$，则它的直角坐标方程为$\frac{{x}^{2}}{5}+{y}^{2}=1$，-$\sqrt{5}$＜x≤$\sqrt{5}$，0≤y≤1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网