题目内容
5.设z=1-i(i为虚数单位),若复数$\frac{2}{z}$-z2在复平面内对应的向量为$\overrightarrow{OZ}$,则向量$\overrightarrow{OZ}$的模是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
分析 把z=1-i代入$\frac{2}{z}$-z2,利用复数代数形式的乘除运算化简,求出复数$\frac{2}{z}$-z2在复平面内对应的点的坐标,的$\overrightarrow{OZ}$的坐标,再由向量模的公式求解.
解答 解:∵z=1-i,∴$\frac{2}{z}$-z2=$\frac{2}{1-i}-(1-i)^{2}=\frac{2(1+i)}{(1-i)(1+i)}+2i=1+3i$,
∴复数$\frac{2}{z}$-z2在复平面内对应的点的坐标为(1,3),向量为$\overrightarrow{OZ}$=(1,3),
则|$\overrightarrow{OZ}$|=$\sqrt{10}$.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,考查了复数模的求法,是基础题.

练习册系列答案
相关题目
13.参数方程$\left\{\begin{array}{l}{x=t}\\{y=1+t}\end{array}\right.$(t为参数)表示曲线是( )
| A. | 一条射线 | B. | 两条射线 | C. | 一条直线 | D. | 两条直线 |
20.执行如图所示的程序框图,则输出m=( )


| A. | 2.25 | B. | 2.5 | C. | 2.625 | D. | 2.75 |
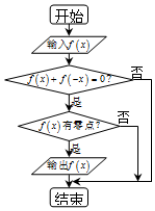 某流程图如图所示,现输入如下四个函数,则可以输出的函数是①②③.
某流程图如图所示,现输入如下四个函数,则可以输出的函数是①②③.