题目内容
2．已知球O是某几何体的外接球，而该几何体是由一个侧棱长为2$\sqrt{5}$的正四棱锥S-ABCD与一个高为6的正四棱柱ABCD-A1B1C1D1拼接而成，则球O的表面积为（ ）| A． | $\frac{100π}{3}$ | B． | 64π | C． | 100π | D． | $\frac{500π}{3}$ |
分析 设球的半径为R，AB=2x，S到平面ABCD的距离为$\sqrt{20-2{x}^{2}}$，列出半径的表达式，由勾股定理可得R2=32+2x2，由此求出R，即可求出球的表面积．
解答 解：设球的半径为R，AB=2x，$\frac{1}{2}AC$=$\sqrt{2}x$，
则球心到平面A1B1C1D1的距离为3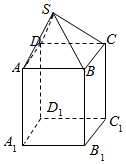
，
几何体是由一个侧棱长为2$\sqrt{5}$的正四棱锥S-ABCD
S到平面ABCD的距离为$\sqrt{（2\sqrt{5}）^{2}-（\sqrt{2}x）^{2}}$=$\sqrt{20-2{x}^{2}}$，
则：$\sqrt{20-2{x}^{2}}$+3=R，
又勾股定理可得R2=32+2x2，
∴R=5，x=2$\sqrt{2}$
∴球的表面积为4πR2=100π．
故选：C．
点评 本题考查球的表面积，考查学生的计算能力，求出球的半径是关键．
练习册系列答案
相关题目
13．参数方程$\left\{\begin{array}{l}{x=t}\\{y=1+t}\end{array}\right.$（t为参数）表示曲线是（ ）
| A． | 一条射线 | B． | 两条射线 | C． | 一条直线 | D． | 两条直线 |
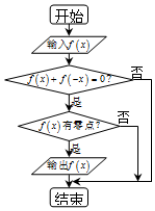某流程图如图所示，现输入如下四个函数，则可以输出的函数是①②③．