题目内容
一组数据从小到大的顺序排列为1,2,2,x,5,10,其中x≠5,已知该数据的中位数是众数的
倍,则该组数据的标准差为( )
| 3 |
| 2 |
| A、3 | B、4 | C、5 | D、6 |
考点:极差、方差与标准差
专题:概率与统计
分析:根据中位数和众数之间的关系,求出x的值,然后利用标准差的公式即可得到结论.
解答:
解:数据的中位数为
,众数为2,
则根据题意,得
=
×2
∴x=4,
则平均数为
(1+2+2+4+5+10)=4,
则数据的方差S2=
[(1-4)2+(2-4)2+(2-4)2+(4-4)2+[(5-4)2+(10-4)2]=
×54=9,
即该组数据的标准差为
=3,
故选:A
| 2+x |
| 2 |
则根据题意,得
| 2+x |
| 2 |
| 3 |
| 2 |
∴x=4,
则平均数为
| 1 |
| 6 |
则数据的方差S2=
| 1 |
| 6 |
| 1 |
| 6 |
即该组数据的标准差为
| 9 |
故选:A
点评:本题主要考查标准差的计算,利用条件求出x的值是解决本题的关键,比较基础.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知实数x、y满足不等式组
,则z=x-y的最小值为( )
|
| A、-1 | ||
B、-
| ||
| C、-3 | ||
| D、3 |
已知直线ax+2y+1=0与直线4x+6y+11=0垂直,则a的值是( )
| A、-5 | B、-1 | C、-3 | D、1 |
已知函数f(x)=
,则下列图象错误的是( )
|
A、 y=f(x-1)的图象 |
B、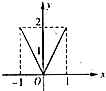 y=f(|x|)的图象 |
C、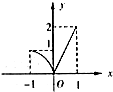 y=f(-x) 的图象 |
D、 y=f(x)的图象 |
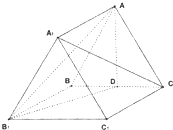 在正三棱柱ABC-A1B1C1中,点D是BC的中点,BC=BB1.
在正三棱柱ABC-A1B1C1中,点D是BC的中点,BC=BB1.


