题目内容
假设你家订了一份早报,送报人可能在早上6:30-7:30之间把报纸送到你家,你父亲离开家去上班的时间在早上7:00-8:00之间,则你父亲离开家前能得到报纸的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:设送报人到达的时间为x,小明爸爸离家去工作的时间为y,则(x,y)可以看成平面中的点,分析可得由试验的全部结果所构成的区域并求出其面积,同理可得事件A所构成的区域及其面积,由几何概型公式,计算可得答案.
解答:
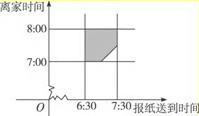 解:设送报人到达的时间为x,小明爸爸离家去工作的时间为y,记小明爸爸离家前能看到报纸为事件A;
解:设送报人到达的时间为x,小明爸爸离家去工作的时间为y,记小明爸爸离家前能看到报纸为事件A;
以横坐标表示报纸送到时间,以纵坐标表示小明爸爸离家时间,建立平面直角坐标系,
小明爸爸离家前能得到报纸的事件构成区域如图示:
由于随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.
根据题意,只要点落到阴影部分,就表示小明爸爸在离开家前能得到报纸,即事件A发生,
所以P(A)=
=
,
故选:C.
 解:设送报人到达的时间为x,小明爸爸离家去工作的时间为y,记小明爸爸离家前能看到报纸为事件A;
解:设送报人到达的时间为x,小明爸爸离家去工作的时间为y,记小明爸爸离家前能看到报纸为事件A;以横坐标表示报纸送到时间,以纵坐标表示小明爸爸离家时间,建立平面直角坐标系,
小明爸爸离家前能得到报纸的事件构成区域如图示:
由于随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.
根据题意,只要点落到阴影部分,就表示小明爸爸在离开家前能得到报纸,即事件A发生,
所以P(A)=
1-
| ||||||
| 1 |
| 7 |
| 8 |
故选:C.
点评:本题考查几何概型的计算,解题的关键在于设出x、y,将(x,y)以及事件A在平面直角坐标系中表示出来,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
若复数z=(m-1)(m-10)+ilgm是纯虚数,其中m是实数,则
=( )
| 2 | ||
|
| A、i | B、-i | C、2i | D、-2i |
如图所示的韦恩图中,阴影部分对应的集合是( )


| A、A∩B |
| B、∁U(A∩B) |
| C、A∩(∁UB) |
| D、(∁UA)∩B |
设p:m≥-2;q:函数f(x)=log2(2x+m)的图象过点(1,2),则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知{an}为等差数列,若a2+a3+a7=12,则S7=( )
| A、24 | B、28 | C、15 | D、54 |
 如图:港口A北偏东30°方向的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31n mile,该轮船从B处沿正西方向航行20n mile后到D处,测得CD为21n mile.
如图:港口A北偏东30°方向的C处有一观测站,港口正东方向的B处有一轮船,测得BC为31n mile,该轮船从B处沿正西方向航行20n mile后到D处,测得CD为21n mile.