题目内容
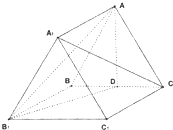 在正三棱柱ABC-A1B1C1中,点D是BC的中点,BC=BB1.
在正三棱柱ABC-A1B1C1中,点D是BC的中点,BC=BB1.(Ⅰ)求证:A1C∥平面 AB1D;
(Ⅱ)求异面直线A1C与B1D所成焦的余弦值;
(Ⅲ)若M为棱CC1的中点,求证:MB⊥AB1.
考点:直线与平面平行的判定,异面直线及其所成的角
专题:空间位置关系与距离
分析:(Ⅰ)证明:连结A1B,交AB1与O,连结OD,O,D均为中点,推断出A1C∥OD,
进而根据线面平行的判定定理得出A1C∥平面AB1D.
(Ⅱ)利用A1C∥OD,推断出∠ODB1为异面直线A1C与BD所成角,令正三棱柱的棱长为1,则DB1,OB1,OD均可求得,利用余弦定理求得cos∠ODB1即可得到答案.
(Ⅲ):依据在正三棱柱ABC-A1B1C1中,BC=BB1,推断出四边形BCC1B1是正方形,通过M为CC1的中点,D是BC的中点,推断出△B1BD≌△BCM,得出∠BB1D=∠CBM,∠BDB1=∠CMB,通过∠BB1D+∠BDB1=
求得∠CBM+∠BDB1=
,进而判断出BM⊥B1D,通过△ABC是正三角形,D是BC的中点,推断出AD⊥BC,利用线面垂直的判定定理推断出AD⊥平面BB1C1C,进而根据线面垂直的性质求得AD⊥BM,进而推断出BM⊥平面AB1D,利用线面垂直的性质可推断出MB⊥AB1.
进而根据线面平行的判定定理得出A1C∥平面AB1D.
(Ⅱ)利用A1C∥OD,推断出∠ODB1为异面直线A1C与BD所成角,令正三棱柱的棱长为1,则DB1,OB1,OD均可求得,利用余弦定理求得cos∠ODB1即可得到答案.
(Ⅲ):依据在正三棱柱ABC-A1B1C1中,BC=BB1,推断出四边形BCC1B1是正方形,通过M为CC1的中点,D是BC的中点,推断出△B1BD≌△BCM,得出∠BB1D=∠CBM,∠BDB1=∠CMB,通过∠BB1D+∠BDB1=
| π |
| 2 |
| π |
| 2 |
解答:
(Ⅰ)证明:连结A1B,交AB1与O,连结OD,
∵O,D均为中点,
∴A1C∥OD,
∵A1C?平面AB1D,OD?平面AB1D,
∴A1C∥平面AB1D.
(Ⅱ)∵A1C∥OD,
∴∠ODB1为异面直线A1C与BD所成角,
令正三棱柱的棱长为1,则DB1=
,OB1=
,OD=
AC=
,
在△ODB1中,cos∠ODB1=
=
,
∴异面直线A1C与B1D所成焦的余弦值为
.
(Ⅲ)证明:∵在正三棱柱ABC-A1B1C1中,BC=BB1,
∴四边形BCC1B1是正方形,
∵M为CC1的中点,D是BC的中点,
∴△B1BD≌△BCM,
∴∠BB1D=∠CBM,∠BDB1=∠CMB,
∵∠BB1D+∠BDB1=
∴∠CBM+∠BDB1=
,
∴BM⊥B1D,
∵△ABC是正三角形,D是BC的中点,
∴AD⊥BC,
∵平面ABC⊥平面BB1C1C,平面ABC∩平面BB1C1C=BC,AD?平面ABC,
∴AD⊥平面BB1C1C,
∵BM?平面BB1C1C,
∴AD⊥BM,
∵AD∩B1D,
∴BM⊥平面AB1D,
∵AB1?平面AB1D,
∴MB⊥AB1.
∵O,D均为中点,
∴A1C∥OD,
∵A1C?平面AB1D,OD?平面AB1D,
∴A1C∥平面AB1D.
(Ⅱ)∵A1C∥OD,
∴∠ODB1为异面直线A1C与BD所成角,
令正三棱柱的棱长为1,则DB1=
| 5 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
在△ODB1中,cos∠ODB1=
O
| ||||
| 2OB1•DB1 |
| ||
| 4 |
∴异面直线A1C与B1D所成焦的余弦值为
| ||
| 4 |
(Ⅲ)证明:∵在正三棱柱ABC-A1B1C1中,BC=BB1,
∴四边形BCC1B1是正方形,
∵M为CC1的中点,D是BC的中点,
∴△B1BD≌△BCM,
∴∠BB1D=∠CBM,∠BDB1=∠CMB,
∵∠BB1D+∠BDB1=
| π |
| 2 |
∴∠CBM+∠BDB1=
| π |
| 2 |
∴BM⊥B1D,
∵△ABC是正三角形,D是BC的中点,
∴AD⊥BC,
∵平面ABC⊥平面BB1C1C,平面ABC∩平面BB1C1C=BC,AD?平面ABC,
∴AD⊥平面BB1C1C,
∵BM?平面BB1C1C,
∴AD⊥BM,
∵AD∩B1D,
∴BM⊥平面AB1D,
∵AB1?平面AB1D,
∴MB⊥AB1.
点评:本题主要考查了线面平行,线面垂直的性质和判定定理.立体几何在求二面角的时候,常转化为平面几何的问题易于解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在等差数列{an}中,已知a3+a9=16,则该数列前11项和S11=( )
| A、58 | B、88 |
| C、143 | D、176 |