题目内容
已知函数f(x)=x2lnx,
(1)求f(x)的极值;
(2)记D={x|f(x)>e2},求当x∈D时,G(x)=
的值域.
(1)求f(x)的极值;
(2)记D={x|f(x)>e2},求当x∈D时,G(x)=
| lnx |
| lnf(x) |
考点:利用导数研究函数的极值,函数的值域
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)确定函数的定义域并求导,从而确定极小值;(2)化简集合D,利用换元法求函数的值域.
解答:
解:(1)函数f(x)的定义域为(0,+∞),
令f′(x)=x(2lnx+1)=0解得,x=
.
在x=
附近,左侧f′(x)<0,右侧f′(x)>0,
则f(x)在x=
上取得极小值-
.
(2)D={x|f(x)>e2}={x|x>e},
令lnx=t(t>1),则lnf(x)=2t+lnt,
G(x)=
=
=
,
令H(t)=
,(t>1)
则H′(t)=
,
则H(t)在(1,e]上单调递增,在[e,+∞)上单调递减;
则H(t)≤H(e)=
,
则2+
≤
,
则
<0或
≥
,
即G(x)的值域为(-∞,0)∪[
,+∞).
令f′(x)=x(2lnx+1)=0解得,x=
| 1 | ||
|
在x=
| 1 | ||
|
则f(x)在x=
| 1 | ||
|
| 1 |
| 2e |
(2)D={x|f(x)>e2}={x|x>e},
令lnx=t(t>1),则lnf(x)=2t+lnt,
G(x)=
| lnx |
| lnf(x) |
| t |
| 2t+lnt |
| 1 | ||
2+
|
令H(t)=
| lnt |
| t |
则H′(t)=
| 1-lnt |
| t2 |
则H(t)在(1,e]上单调递增,在[e,+∞)上单调递减;
则H(t)≤H(e)=
| 1 |
| e |
则2+
| lnt |
| t |
| 2e+1 |
| e |
则
| 1 | ||
2+
|
| 1 | ||
2+
|
| e |
| 2e+1 |
即G(x)的值域为(-∞,0)∪[
| e |
| 2e+1 |
点评:本题考查了导数的应用,注意函数的定义域;利用换元法求值域时要注意其取值范围.

练习册系列答案
相关题目
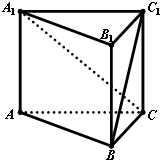 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.