题目内容
下列命题:
①“a>b”是“ac2>bc2”的必要条件;
②对于椭圆来说,离心率e越大椭圆越圆,离心率越小,椭圆越扁;
③给定两个命题p,q,若p是¬q的充分不必要条件,则¬p也是q的充分不必要条件;
④若空间任意一点O和不共线的三点A,B,C,满足向量关系式:
=x
+y
+z
,则P,A,B,C四点共面的充要条件是:x+y+z=1.
其中所有真命题的序号是: .
①“a>b”是“ac2>bc2”的必要条件;
②对于椭圆来说,离心率e越大椭圆越圆,离心率越小,椭圆越扁;
③给定两个命题p,q,若p是¬q的充分不必要条件,则¬p也是q的充分不必要条件;
④若空间任意一点O和不共线的三点A,B,C,满足向量关系式:
| OP |
| OA |
| OB |
| OC |
其中所有真命题的序号是:
考点:命题的真假判断与应用
专题:简易逻辑
分析:①由“ac2>bc2”可得a>b,反之不成立;
②对于椭圆来说,离心率e越小椭圆越圆,离心率越大,椭圆越扁,即可判断出;
③给定两个命题p,q,若p是¬q的充分不必要条件,则¬p也是q的必要不充分条件;
④若空间任意一点O和不共线的三点A,B,C,满足向量关系式:
=x
+y
+z
,则P,A,B,C四点共面的充要条件是:x+y+z=1,由向量共面定理即可判断出.
②对于椭圆来说,离心率e越小椭圆越圆,离心率越大,椭圆越扁,即可判断出;
③给定两个命题p,q,若p是¬q的充分不必要条件,则¬p也是q的必要不充分条件;
④若空间任意一点O和不共线的三点A,B,C,满足向量关系式:
| OP |
| OA |
| OB |
| OC |
解答:
解:①由“ac2>bc2”可得a>b,反之不成立,因此“a>b”是“ac2>bc2”的必要条件,正确;
②对于椭圆来说,离心率e越小椭圆越圆,离心率越大,椭圆越扁,因此②不正确;
③给定两个命题p,q,若p是¬q的充分不必要条件,则¬p也是q的必要不充分条件,因此不正确;
④若空间任意一点O和不共线的三点A,B,C,满足向量关系式:
=x
+y
+z
,则P,A,B,C四点共面的充要条件是:x+y+z=1,正确.
综上可得:其中所有真命题的序号是:①④.
故答案为:①④.
②对于椭圆来说,离心率e越小椭圆越圆,离心率越大,椭圆越扁,因此②不正确;
③给定两个命题p,q,若p是¬q的充分不必要条件,则¬p也是q的必要不充分条件,因此不正确;
④若空间任意一点O和不共线的三点A,B,C,满足向量关系式:
| OP |
| OA |
| OB |
| OC |
综上可得:其中所有真命题的序号是:①④.
故答案为:①④.
点评:本题综合考查了椭圆的离心率的性质、不等式的性质、充分必要条件、向量共面定理等基础知识与基本技能方法,考查了推理能力,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
已知a1=1,a2=-
,a3=-
,…,an+1=-
,….那么a2014=( )
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
| A、-2 | ||
B、-
| ||
| C、1 | ||
| D、2 |
若0<α<2π,则使sinα<
和cosα>
同时成立的α的取值范围是( )
| ||
| 2 |
| 1 |
| 2 |
A、(-
| ||||
B、(0,
| ||||
C、(
| ||||
D、(0,
|
已知两点O(0,0)、A(1,1)及直线l:x+y=a,它们满足:O、A有一点在直线l上或O、A在直线l的两侧.设h(a)=a2+2a+3,则使不等式x2+4x-2≤h(a)恒成立的x的取值范围是( )
| A、[0,2] |
| B、[-5,1] |
| C、[3,11] |
| D、[2,3] |
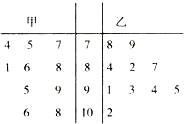 某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.
某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.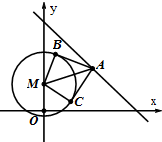 已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.
已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.